2022-2023學年江蘇省無錫一中高一（下）期末數學試卷

一.單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個

• 1．已知i為虛數單位，復數

  5

  i

  +

  2

  的共軛復數為（　　）

  A．i+2

  B．i-2

  C．-2-i

  D．2-i
  組卷：100引用：2難度：0.8

  解析

• 2．△ABC中，

  AD

  =

  1

  3

  AB

  ，點E是CD的中點，設

  AB

  =

  a

  ，

  AC

  =

  b

  ，則

  AE

  =（　　）

  A． 1 2 a + 1 6 b

  B． 1 6 a + 2 3 b

  C． 1 2 a + 1 3 b

  D． 1 6 a + 1 2 b
  組卷：265引用：11難度：0.7

  解析

• 3．已知a,b,l是不同的直線，α，β是不同的平面，則下列結論成立的是（　　）

  A．若a?α，b?β，則a與b是異面直線

  B．若α⊥β，α∩β=l,a⊥l,則a⊥α

  C．若l⊥a,l⊥b,a,b?α，則l⊥α

  D．若α∥β，a?α，則a∥β
  組卷：131引用：1難度：0.6

  解析

• 4．某工廠隨機抽取20名工人，對他們某天生產的產品件數進行統計，數據如表，
  

  件數	7	8	9	10	11
  人數	3	7	5	4	1

  則該組數據的上四分位數（第75百分位數）是（　　）

  A．8.5

  B．9

  C．9.5

  D．10
  組卷：122引用：1難度：0.8

  解析

• 5．若 P（AB）=

  1

  18

  ，P（

  A

  ）=

  1

  3

  ，P（B）=

  1

  12

  ，則事件A與B的關系是（　　）

  A．事件A與B互斥但不對立

  B．事件A與B對立

  C．事件A與B相互獨立

  D．事件A與B既互斥又相互獨立
  組卷：253引用：2難度：0.7

  解析

• 6．PA、PB、PC是從P點出發的三條射線，每兩條射線的夾角均為60°，那么直線PC與平面PAB所成角的余弦值是（　　）

  A． 1 2

  B． 2 2

  C． 3 3

  D． 6 3
  組卷：897引用：29難度：0.7

  解析

• 7．如圖，平面四邊形ABCD中，△BCD是等邊三角形，AB⊥BD，且AB=BD=2，M是AD的中點．沿BD將△BCD翻折，折成三棱錐 C-ABD，在翻折中，下列結論正確的是（　　）
  

  A．三棱錐C-ABD的體積最大為 2 3

  B．存在某個位置，使得CM與BD所成角為銳角

  C．當平面ABD⊥平面BDC時，三棱錐C-ABD的外接球的表面積是 28 π 3

  D．∠CMB一定是二面角 C-AD-B 的平面角
  組卷：273引用：1難度：0.5

  解析

四.解答題：本題共6小題、17題10分，其余每小題10分共70分.解答應寫出文字說明、證明過程或演算步驟.

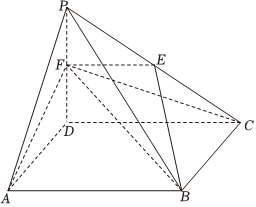• 21．如圖，在四棱錐P-ABCD中，底面ABCD是矩形，PD⊥底面ABCD，且 PD=AD=2，E是PC的中點，平面ABE與線段PD交于點F．
  （1）證明：F為PD的中點；
  （2）若三棱錐P-BCF的體積為1，求平面CFB與平面AFB夾角的余弦值．
  組卷：305引用：1難度：0.5

  解析

• 22．已知a,b,c分別為△ABC三個內角A，B，C的對邊，且acosC+

  3

  asinC-b-c=0，a=

  13

  ，且△ABC的面積為

  3

  ．
  （1）求b+c；
  （2）若b＞c,N為AC的中點，M為BC的三等分點（BM＜MC），P為AM與BN的交點，求∠BPA的余弦值及MP²+NP²的值．
  組卷：179引用：1難度：0.4

  解析