當前位置：試卷中心 > 試卷詳情

2024年遼寧省新中考數學試卷（樣卷）

發布：2024/10/25 0:0:1

一、選擇題（本題共10小題，每小題3分，共30分．在每小題給出的四個選項中，只有一項是符合題目要求的）

1．某校儀仗隊隊員的平均身高為175cm,如果高于平均身高2cm記作+2cm,那么低于平均身高2cm應該記作（　　）
A．2cm B．-2cm C．175cm D．-175cm
組卷：1977引用：11難度：0.9
解析
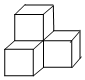2．如圖是由4個相同的小立方體搭成的幾何體，這個幾何體的主視圖是（　　）
A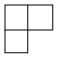． B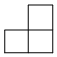． C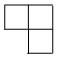． D．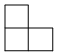
組卷：422引用：8難度：0.8
解析
3．下列圖形既是軸對稱圖形又是中心對稱圖形的是（　　）
A． B． C． D．
組卷：532引用：5難度：0.9
解析
4．下列運算正確的是（　　）
A．2a+4=6a B．a²?a³=a⁵ C．（2a）²=2a² D．a³÷a³=a
組卷：1963引用：24難度：0.8
解析
5．關于一元二次方程x²-2x-1=0根的情況，下列說法正確的是（　　）
A．有一個實數根 B．有兩個相等的實數根
C．有兩個不相等的實數根 D．沒有實數根
組卷：8引用：13難度：0.7
解析
6．解分式方程
2
x
=
1
x
-
1
時，將方程兩邊都乘同一個整式．得到一個一元一次方程，這個整式是（　　）
A．x B．x-1 C．x（x+1） D．x（x-1）
組卷：570引用：4難度：0.7
解析
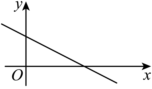7．一次函數y=kx+2的圖象如圖所示，下列結論正確的是（　　）
A．k＜0
B．y隨x增大而增大
C．圖象經過原點
D．圖象經過第一、二、三象限
組卷：1553引用：7難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本題共8小題，共75分．解答應寫出文字說明、演算步驟或推理過程）

22．【發現問題】

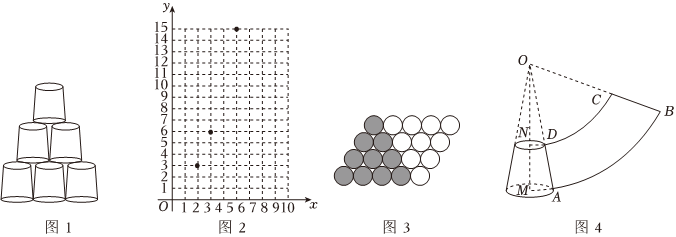
“速疊杯”是深受學生喜愛的一項運動，杯子的疊放方式如圖1所示：每層都是杯口朝下排成一行，自下向上逐層遞減一個杯子，直至頂層只有一個杯子．愛思考的小麗發現疊放所需杯子的總數隨著第一層（最底層）杯子的個數變化而變化．
【提出問題】
疊放所需杯子的總數y與第一層杯子的個數x之間有怎樣的函數關系？
【分析問題】
小麗結合實際操作和計算得到下表所示的數據：

第一層杯子的個數x 1 2 3 4 5 …

杯子的總數y 1 3 6 10 15 …

然后在平面直角坐標系中，描出上面表格中各對數值所對應的點，得到圖2，小麗根據圖2中點的分布情況，猜想其圖象是二次函數圖象的一部分；為了驗證自己的猜想，小麗從“形”的角度出發，將要計算總數的杯子用黑色圓表示（如圖3），再借助“補”的思想，補充相同數量的白色圓，使每層圓的數量相同，進而求出y與x的關系式．
【解決問題】
（1）直接寫出y與x的關系式；
（2）現有36個杯子，按【發現問題】中的方式疊放，求第一層杯子的個數；
（3）杯子的側面展開圖如圖4所示，ND，MA分別為上、下底面圓的半徑，
?
AB
所對的圓心角∠AOB=60°，OA=24cm,OD=15cm.將這樣足夠數量的杯子按【發現問題】中的方式疊放，但受桌面長度限制，第一層擺放杯子的總長度不超過80cm,求杯子疊放達到的最大高度和此時杯子的總數．（提示：杯子下底面圓周長與AB的長度相等）
組卷：920引用：4難度：0.4
解析
23．【問題初探】
（1）在數學活動課上，李老師給出如下問題：如圖1，在△ACD中，∠D=2∠C，AB⊥CD，垂足為B，且BC＞AB．求證：BC=AD+BD．

①如圖2，小鵬同學從結論的角度出發給出如下解題思路：在BC上截取BE=BD，連接AE，將線段BC與AD，BD之間的數量關系轉化為AD與CE之間的數量關系．
②如圖3，小亮同學從∠D=2∠C這個條件出發給出另一種解題思路：作AC的垂直平分線，分別與AC，CD交于F，E兩點，連接AE，將∠D=2∠C轉化為∠D與∠BEA之間的數量關系．
請你選擇一名同學的解題思路，寫出證明過程．
【類比分析】
（2）李老師發現之前兩名同學都運用了轉化思想，將證明三條線段的關系轉化為證明兩條線段的關系；為了幫助學生更好地感悟轉化思想，李老師將圖1進行變換并提出了下面問題，請你解答．
如圖4，在Rt△ABC中，∠ABC=90°，過點A作AD∥BC（點D與點C在AB同側），若∠ADB=2∠C．求證：BC=AD+BD．
【學以致用】
（3）如圖5，在四邊形ABCD中，
AD
=
100
3
，
CD
=
121
3
，
sin
D
=
3
5
，
∠
BCD
=∠
BAD
，
∠
ABC
=
3
∠
ADC
，求四邊形ABCD的面積．
組卷：1043引用：2難度：0.6
解析