當前位置：試卷中心 > 試卷詳情

2022-2023學年四川省眉山市高二（下）期末數學試卷（文科）

發布：2024/6/26 8:0:9

1．若復數z滿足
z
-
1
=
3
+
i
i
，則z的虛部等于（　　）
A．3i B．3 C．-3i D．-3
組卷：6引用：2難度：0.8
解析
2．某學校為了解高二（1）班的30名的身體素質，將這些學生編號為1，2，…30，從這些學生中用系統抽樣方法等距抽取5名學生進行體質測試．若20號學生被抽到，則下面4名學生中被抽到的是（　　）
A．5號學生 B．12號學生 C．14號學生 D．25號學生
組卷：18引用：2難度：0.6
解析
3．我國數學家陳景潤在哥德巴赫猜想的研究中取得了世界領先的成果．哥德巴赫猜想是“每個大于2的偶數可以表示為兩個素數的和”，如30=7+23．在不超過30的素數中，隨機選取兩個不同的數，其和等于30的概率是（　　）
A．
1
12
B．
1
14
C．
1
15
D．
1
18
組卷：4546引用：27難度：0.7
解析
4．已知函數y=f（x）的圖像在點（2，f（2））處的切線方程是x-2y+4=0，則f（2）+f′（2）的值是（　　）
A．
3
2
B．
7
2
C．
5
2
D．3
組卷：40引用：2難度：0.8
解析

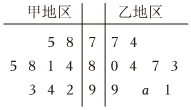5．某市質量檢測部門從轄區內甲、乙兩個地區的食品生產企業中分別隨機抽取9家企業，根據食品安全管理考核指標對抽到的企業進行考核，并將各企業考核得分整理成如下的莖葉圖．由莖葉圖所給信息，可判斷以下結論中正確是（　　）

A．若a=2，則甲地區考核得分的極差大于乙地區考核得分的極差

B．若a=4，則甲地區考核得分的平均數小于乙地區考核得分的平均數

C．若a=5，則甲地區考核得分的方差小于乙地區考核得分的方差

D．若a=6，則甲地區考核得分的中位數小于乙地區考核得分的中位數

組卷：52引用：4難度：0.7

6．已知函數f（x）的導函數為f′（x）=x+sinx,且
f
（
1
）
=
1
3
，則f（-1）=（　　）
A．
1
3
-
cos
1
B．
1
3
+
cos
1
C．
-
1
3
D．
1
3
組卷：24引用：2難度：0.7
解析
7．用秦九韶算法求多項式f（x）=x⁵+x⁴+2x³+3x²+x+1在x=3時，v₃的值為（　　）
A．136 B．45 C．27 D．14
組卷：29引用：2難度：0.8
解析

21．已知函數f（x）=ax²-2lnx.
（1）當a=1時，求y=f（x）在點（1，f（1））處的切線方程；
（2）若對?x∈[1，3]，都有
f
（
x
）
≤
1
4
恒成立，求a的取值范圍．
組卷：117引用：3難度：0.4
解析
22．已知函數f（x）=e^x-a-x-cosx,x∈（-π，π）其中e=2.71828?為自然對數的底數．
（1）當a=0時，證明：f（x）≥0；
（2）當a=1時，求函數y=f（x）零點個數．
組卷：18引用：2難度：0.3
解析