2022-2023學年遼寧省名校聯盟高二（下）月考數學試卷（3月份）

一、選擇題。本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合M={x|-4＜x＜3}，N={x|x＜-1}，則M∪（?_RN）=（　　）

  A．{x|x＜3}

  B．{x|x＞-4}

  C．{x|-1≤x＜3}

  D．R
  組卷：94引用：2難度：0.8

  解析

• 2．已知

  z

  =

  （

  2

  -

  1

  i

  3

  ）

  ?

  i

  ，則

  z

  =（　　）

  A．2+i

  B．2-i

  C．1+2i

  D．1-2i
  組卷：23引用：2難度：0.8

  解析

• 3．我國數學家陳景潤在哥德巴赫猜想的研究中取得了世界領先的成果，哥德巴赫猜想是1742年哥德巴赫給數學家歐拉的信中提出的猜想：“任意大于2的偶數都可以表示成兩個質數之和”，則哥德巴赫猜想的否定為（　　）

  A．任意小于2的偶數都不可以表示成兩個質數之和

  B．任意大于2的偶數都不可以表示成兩個質數之和

  C．至少存在一個小于2的偶數不可以表示成兩個質數之和

  D．至少存在一個大于2的偶數不可以表示成兩個質數之和
  組卷：118引用：4難度：0.7

  解析

• 4．已知角θ的頂點為坐標原點，始邊與x軸的非負半軸重合，其終邊經過點（-2，-1），則tan3θ=（　　）

  A． 11 2

  B． 9 2

  C． 7 2

  D． 5 2
  組卷：49引用：3難度：0.7

  解析

• 5．已知圓C經過點M（1，2），N（3，0），則點P（2，-1）到圓心C的距離的最小值為（　　）

  A．2

  B． 3

  C． 2

  D．1
  組卷：220引用：3難度：0.8

  解析

• 6．已知某N95口罩廠的一條生產流水線上有編號依次為①至⑥的6個不同質檢站，現將甲、乙、丙等6名質檢員安排到這6個不同質檢站進行產品檢測，每個質檢站安排1人，丙不在①和⑥質檢站，則甲、乙所在質檢站的編號相鄰的概率為（　　）

  A． 2 5

  B． 3 10

  C． 1 5

  D． 1 10
  組卷：78引用：2難度：0.5

  解析

• 7．已知直三棱柱：ABC-A₁B₁C₁的底面為等腰直角三角形，AC=BC，AA₁=AB=2，E，F分別為AB，BB₁的中點，M為CC₁上一點，C₁M=3MC，則異面直線ME與A₁F所成角的余弦值為（　　）

  A． 1 5

  B． 1 4

  C． 2 5

  D． 1 3
  組卷：83引用：3難度：0.5

  解析

四、解答題。本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

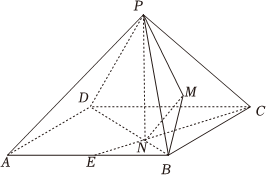• 21．如圖，正四棱錐P-ABCD的棱長均為

  2

  2

  ，點M為△PBC的中心，E為AB的中點，BD與CE交于點N．
  （1）證明：MN∥平面PAB；
  （2）求二面角B-MN-P的正弦值．
  組卷：79引用：2難度：0.5

  解析

• 22．已知F₁，F₂為雙曲線

  E

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦點，E的一條漸近線方程為y=3x,M為E上一點，且|MF₁|-|MF₂|=-2．
  （1）求E的方程；
  （2）設點M在坐標軸上，直線l與E交于異于M的A，B兩點，N為AB的中點，且|AB|=2|MN|，過M作MC⊥AB，垂足為C，是否存在點D，使得|CD|為定值？若存在，求出點D的坐標以及|CD|的長度；若不存在，請說明理由．
  組卷：39引用：2難度：0.5

  解析