2022-2023學年黑龍江省哈爾濱九中高二（下）月考數學試卷（6月份）

一、單選題：本題共有8個小題，每小題5分，共40分，在每小題給出的四個選項中是符合題目要求的．

• 1．已知f（x）=xlnx,則曲線y=f（x）在點（1，f（1））處的切線方程為（　　）

  A．x-y-1=0

  B．x-y-2=0

  C．x+y-1=0

  D．x+y-2=0
  組卷：85引用：2難度：0.8

  解析

• 2．對于定義在R上的可導函數f（x），f′（x）為其導函數，下列說法正確的是（　　）

  A．使f'（x）=0的x一定是函數的極值點

  B．f（x）在R上單調遞增是f'（x）＞0在R上恒成立的充要條件

  C．若函數f（x）既有極小值又有極大值，則其極小值一定不會比它的極大值大

  D．若f（x）在R上存在極值，則它在R一定不單調
  組卷：63引用：2難度：0.6

  解析

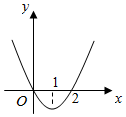• 3．設f'（x）是函數f（x）的導函數，y=f'（x）的圖象如圖所示，則y=f（x）的圖象最有可能的是（　　）

  A．

  B．

  C．

  D．
  組卷：1149引用：32難度：0.7

  解析

• 4．函數

  f

  （

  x

  ）

  =

  1

  3

  x

  3

  +

  1

  2

  a

  x

  2

  +

  x

  -

  1

  存在兩個極值點，則實數a的取值范圍是（　　）

  A．（-∞，-2）∪（2，+∞）	B．（-∞，-2]∪[2，+∞）
  C．（-2，2）	D．[-2，2]
  組卷：47引用：2難度：0.6

  解析

• 5．設點P在曲線

  y

  =

  lnx

  -

  1

  x

  +

  1

  上，點Q在直線y=2x上，則PQ的最小值為（　　）

  A．2

  B．1

  C． 6 5

  D． 2 5 5
  組卷：235引用：3難度：0.6

  解析

• 6．定義在R上的可導函數f（x）的導函數為f′（x），滿足f′（x）＞f（x），f（0）=1，則不等式f（x）＜e^x的解集為（　　）

  A．（-∞，6）

  B．（6，+∞）

  C．（0，+∞）

  D．（-∞，0）
  組卷：44引用：3難度：0.7

  解析

• 7．已知

  a

  =

  ln

  2

  2

  ，

  b

  =

  ln

  3

  6

  ，

  c

  =

  1

  2

  e

  ，則a,b,c的大小為（　　）

  A．b＞c＞a

  B．a＞b＞c

  C．b＞a＞c

  D．c＞b＞a
  組卷：681引用：8難度：0.5

  解析

四、解答題：本題共有6個小題，共70分．

• 21．已知a∈R，函數

  f

  （

  x

  ）

  =

  a

  x

  +

  lnx

  ,

  g

  （

  x

  ）

  =

  ax

  -

  lnx

  -

  2

  ．
  （1）當f（x）與g（x）都存在極小值，且極小值之和為0時，求實數a的值；
  （2）當a=1時，若f（x₁）=f（x₂）=b（x₁≠x₂），求證：x₁+x₂＞2
  組卷：38引用：1難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  klnx

  +

  1

  e

  x

  （

  k

  ∈

  R

  ）

  ．
  （1）若函數y=f（x）在（2，3）上不單調，求k的取值范圍；
  （2）已知0＜x₁＜x₂．
  （ⅰ）證明：

  e

  e

  x

  2

  -

  e

  e

  x

  1

  ＞

  -

  ln

  x

  2

  x

  1

  ＞

  1

  -

  x

  2

  x

  1

  ；
  （ⅱ）若

  x

  1

  e

  x

  1

  =

  x

  2

  e

  x

  2

  =

  k

  ，證明：|f（x₁）-f（x₂）|＜1．
  組卷：17引用：1難度：0.5

  解析