2023-2024學年四川省成都市錦江區名校高三（上）開學數學試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項符合題目要求的．

• 1．已知集合A={x|x²+2x≤0}，

  B

  =

  {

  a

  |

  ?

  x

  ∈

  R

  ，

  x

  2

  -

  ax

  +

  1

  4

  ＜

  0

  }

  ，則A∩B=（　　）

  A．[1，2）

  B．[-2，-1]

  C．[-2，1）

  D．[-2，-1）
  組卷：57引用：3難度：0.8

  解析

• 2．復數z在復平面內對應的點為（2，1），則

  2

  i

  z

  -

  1

  =（　　）

  A．1+i

  B．1-i

  C．-1+i

  D．-1-i
  組卷：221引用：9難度：0.8

  解析

• 3．已知向量

  a

  =

  （

  1

  ，

  m

  ）

  ，

  b

  =

  （

  -

  1

  ，

  0

  ）

  ，且

  |

  a

  -

  b

  |

  =

  a

  ?

  b

  +

  6

  ，則

  |

  a

  |

  =（　　）

  A． 5

  B． 2 3

  C． 22

  D． 2 6
  組卷：403引用：10難度：0.7

  解析

• 4．部分與整體以某種相似的方式呈現稱為分形，一個數學意義上分形的生成是基于一個不斷迭代的方程式，即一種基于遞歸的反饋系統，分形幾何學不僅讓人們感悟到科學與藝術的融合，數學與藝術審美的統一，而且還有其深刻的科學方法論意義，如圖，由波蘭數學家謝爾賓斯基1915年提出的謝爾賓斯基三角形就屬于一種分形，具體作法是取一個實心三角形，沿三角形的三邊中點連線．將它分成4個小三角形，去掉中間的那一個小三角形后，對其余3個小三角形重復上述過程逐次得到各個圖形．
  
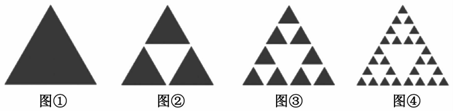
  若記圖①三角形的面積為

  3

  4

  ，則第n個圖中陰影部分的面積為（　　）

  A． 3 9 ? （ 3 2 ） n + 1

  B． 3 6 ? （ 3 2 ） n

  C． 3 4 ? （ 3 4 ） n

  D． 3 3 ? （ 3 4 ） n
  組卷：91引用：7難度：0.7

  解析

• 5．已知矩形ABCD中，AB=2BC，現向矩形ABCD內隨機投擲質點P，則滿足∠APB為銳角的概率是（　　）

  A． 4 - π 4

  B． π 4

  C． 16 - π 16

  D． π 16
  組卷：114引用：7難度：0.8

  解析

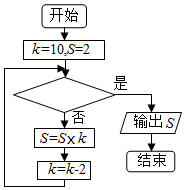• 6．在如圖所示的程序框圖中，程序運行的結果S為3840，那么判斷框中可以填入的關于k的判斷條件是（　　）

  A．k＜5

  B．k＞5

  C．k＜4

  D．k＞4
  組卷：39引用：10難度：0.7

  解析

• 7．在2023年成都大運會期間，組委會派遣甲、乙、丙、丁、戍五名志愿者參加A，B，C三個場館的翻譯工作，每人只去1個場館，每個場館至少去1人，且甲、乙兩人約定去同一個場館，則不同的派遣方案共有（　　）

  A．24種

  B．36種

  C．48種

  D．64種
  組卷：44引用：2難度：0.7

  解析

（二）選考題：共10分．請考生在第22，23題中任選一題作答，如果多做，則按所做的第一題計分．

• 22．直角坐標系xOy中，點P（0，1），動圓C：（x-sinα）²+（y-3sinα-1）²=1（α∈R）．
  （1）求動圓圓心C的軌跡；
  （2）以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線M的極坐標方程為：

  ρ

  2

  =

  2

  2

  co

  s

  2

  θ

  +

  si

  n

  2

  θ

  ，過點P的直線l與曲線M交于A，B兩點，且

  |

  |

  PA

  |

  -

  |

  PB

  |

  |

  =

  4

  7

  ，求直線l的斜率．
  組卷：109引用：8難度：0.6

  解析

• 23．已知函數f（x）=|2x+3|+|2x-2|，g（x）=sin2x.
  （1）求函數f（x）+g（x）的最小值；
  （2）設a,b∈（-1，1），求證：|2a+1|-|1-2b|＜|2ab+2|．
  組卷：15引用：11難度：0.5

  解析