2021-2022學年江西科技學院附中高二（下）第一次月考數學試卷（文科）

一、選擇題（本大題共12小題，每小題5分，共60分）

• 1．“直線m垂直平面α內的無數條直線”是“m⊥α”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：294引用：4難度：0.8

  解析

• 2．
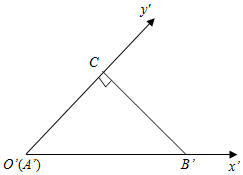
  如圖，△A'B'C'是水平放置的△ABC的斜二測直觀圖，△A'B′C′為等腰直角三角形，其中O′與A′重合，A'B′=6，則△ABC的面積是（　　）

  A．9

  B．9 2

  C．18

  D．18 2
  組卷：448引用：6難度：0.7

  解析

• 3．設m,n是兩條不同的直線，α，β，γ是三個不同的平面，給出下列四個命題：
  ①若m⊥α，n∥α，則m⊥n
  ②若α∥β，β∥γ，m⊥α，則m⊥γ
  ③若m∥α，n∥α，則m∥n
  ④若α⊥γ，β⊥γ，則α∥β
  其中正確命題的序號是（　　）

  A．①和②

  B．②和③

  C．③和④

  D．①和④
  組卷：644引用：115難度：0.9

  解析

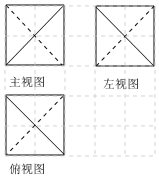• 4．某三棱錐的三視圖如圖所示，其中網格由邊長為1的小正方形組成，則該幾何體的表面積為（　　）

  A． 8 3

  B． 6 3

  C． 4 3

  D． 2 3
  組卷：74引用：2難度：0.6

  解析

• 5．已知A，B，C為球O的球面上的三個點，⊙O₁為△ABC的外接圓．若⊙O₁的面積為4π，AB=BC=AC=OO₁，則球O的表面積為（　　）

  A．64π

  B．48π

  C．36π

  D．32π
  組卷：9546引用：39難度：0.6

  解析

• 6．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  與圓x²+y²=b²在第二象限相交于點M，F₁，F₂分別為該雙曲線的左、右焦點，且sin∠MF₁F₂=3sin∠MF₂F₁，則該雙曲線的離心率為（　　）

  A． 2

  B． 3 2

  C． 3

  D．2
  組卷：191引用：4難度：0.4

  解析

• 7．《九章算術?商功》：“斜解立方，得兩塹堵，斜解塹堵，其一為陽馬，一為鱉臑．陽馬居二，鱉臑居一，不易之率也．合兩鱉臑三而一，驗之以基，其形露矣．”文中“陽馬”是底面為長方形且有一條側棱與底面垂直的四棱錐．在陽馬P-ABCD中，側棱PA⊥底面ABCD，且PA=1，AB=AD=2，則點A到平面PBD的距離為（　　）

  A． 2 3

  B． 6 3

  C． 6 2

  D． 3 3
  組卷：84引用：6難度：0.7

  解析

選考題：共10分，請考生在第22、23題中任選一題作答。如果多做，則按所做的第一題計分。[選修4-4：坐標系與參數方程]

• 22．已知在平面直角坐標系xOy中，直線l的參數方程為

  x = 2 - t

  y = 1 + t

  （t為參數），曲線C₁的方程為x²+y²-x=0，以坐標原點為極點，x軸的正半軸為極軸建立極坐標系．
  （1）求直線l和曲線C₁的極坐標系方程；
  （2）曲線C₂：θ=α（ρ＞0，0＜α＜

  π

  2

  ）分別交直線l和曲線C₁于M，N，求

  3

  |

  OM

  |

  +|ON|的最大值．
  組卷：201引用：10難度：0.6

  解析

[選修4-5：不等式選講]

• 23．已知f（x）=|x+

  3

  2

  |+|1-2x|．
  （1）解不等式f（x）≤

  7

  2

  -x；
  （2）令f（x）的最小值為M，正數a,b滿足a+2b=M，求證：a²b²+

  2

  ab

  ≥

  17

  4

  ．
  組卷：23引用：3難度：0.4

  解析