2022-2023學年湖南省湘潭市兩校高二（上）期末數學試卷

一、單選題（本大題共8小題，共40分）

• 1．已知在空間四邊形ABCD中，

  CG

  =

  1

  2

  CD

  ，則

  BD

  +

  BC

  +

  2

  AB

  =（　　）

  A．2 AG

  B．2 GC

  C．2 BC

  D． 1 2 BC
  組卷：255引用：5難度：0.8

  解析

• 2．若直線l的斜率為k,且k²=3，則直線l的傾斜角為（　　）

  A．30°或150°

  B．45°或135°

  C．60°或120°

  D．90°或180°
  組卷：198引用：4難度：0.7

  解析

• 3．已知△ABC的三個頂點是A（-3，0），B（6，2），C（0，-6），則邊AC上的高所在的直線方程為（　　）

  A．x+2y-2=0

  B．x-2y-2=0

  C．x-2y-4=0

  D．2x+y-14=0
  組卷：357引用：2難度：0.7

  解析

• 4．由倫敦著名建筑事務所SteynStudio設計的南非雙曲線大教堂驚艷世界，該建筑是數學與建筑完美結合造就的藝術品．若將如圖所示的大教堂外形弧線的一段近似看成雙曲線

  y

  2

  a

  2

  -

  x

  2

  b

  2

  =

  1

  （a＞0，b＞0）下支的部分，且此雙曲線兩條漸近線方向向下的夾角為60°，則該雙曲線的離心率為（　　）

  A． 3 3

  B． 3

  C． 3 2

  D． 2 3 3
  組卷：146引用：5難度：0.6

  解析

• 5．已知圓C：x²+y²+4x-8y+12=0，過點P（-4，-2）作圓C的切線PA，PB，切點為A，B，則△ABC的面積為（　　）

  A． 4 5

  B． 8 5

  C． 16 5

  D． 32 5
  組卷：126引用：2難度：0.5

  解析

• 6．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的兩條漸近線與拋物線y²=8x的準線分別交于M，N兩點，A為雙曲線的右頂點，若雙曲線的離心率為2，且△AMN為正三角形，則雙曲線的方程為（　　）

  A． x 2 8 - y 2 24 = 1	B． x 2 16 - y 2 48 = 1
  C． x 2 24 - y 2 72 = 1	D． x 2 64 - y 2 192 = 1
  組卷：40引用：1難度：0.7

  解析

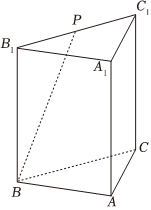• 7．《九章算術》是我國東漢初年編訂的一部數學經典著作，其在卷第五《商功》中記載“斜解立方，得兩塹堵”，塹堵是底面為直角三角形的直三棱柱．如圖，在塹堵ABC-A₁B₁C₁中，AB=AC=AA₁=1，P為B₁C₁的中點，則

  A

  C

  1

  ?

  BP

  =（　　）

  A． 3 2

  B．1

  C． 3 4

  D． 1 2
  組卷：69引用：3難度：0.7

  解析

四、解答題（本大題共6小題，共70分，17題為10分，18至22題為12分）

• 21．已知橢圓E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）經過三點（0，1），（1，1），

  （

  -

  2

  ，

  0

  ）

  中的兩點．
  （1）求E的方程；
  （2）過E的右焦點的直線l與E交于A，B兩點，在直線x=2上是否存在一點D，使得△ABD是以AB為斜邊的等腰直角三角形？若存在，求出l的方程；若不存在，請說明理由．
  組卷：171引用：6難度：0.5

  解析

• 22．已知過點A（-1，0）的直線與拋物線C：y²=2px（p＞0）交于不同的兩點M，N，過點M的直線交C于另一點Q，直線MQ斜率存在且過點B（1，-1），拋物線C的焦點為F，△ABF的面積為1．
  （Ⅰ）求拋物線C的方程．
  （Ⅱ）問：直線QN是否過定點？若過定點，請求出定點的坐標；若不過定點，請說明理由．
  組卷：58引用：3難度：0.6

  解析