當前位置：試卷中心 > 試卷詳情

2022-2023學年江西省撫州市崇仁一中、廣昌一中、金溪一中高二（上）第二次聯考數學試卷

發布：2024/7/23 8:0:8

一、單選題（本大題共8小題，每小題5分，共40分）

1．若空間向量
BA
=
（
1
，
4
，
1
）
，
BC
=
（
2
，
0
，-
2
）
，則
AC
=（　　）
A．（1，-4，-3） B．（1，-3，-4） C．（3，4，-1） D．（-1，4，3）
組卷：188引用：5難度：0.8
解析
2．已知某居民小區附近設有A，B，C，D4個核酸檢測點，居民可以選擇任意一個點位去做核酸檢測，現該小區的3位居民要去做核酸檢測，則檢測點的選擇共有（　　）
A．64種 B．81種 C．7種 D．12種
組卷：266引用：3難度：0.9
解析
3．設a∈R，若直線l₁：ax+2y-8=0與直線l₂：x+（a+1）y+5=0平行，則a的值為（　　）
A．1 B．-2 C．1或-2 D．-
2
3
組卷：180引用：5難度：0.8
解析
4．過點P（-
3
，-1）的直線l與圓x²+y²=1有公共點，則直線l傾斜角的取值范圍是（　　）
A．（0，
π
6
] B．[0，
π
3
] C．[0，
π
6
] D．（0，
π
3
]
組卷：301引用：12難度：0.5
解析
5．為了紀念高中三年舍友之間留下的深厚情感，某宿舍的7位同學決定站成一排合照留念，其中中間位置只能站甲或乙，且甲、乙、丙三人不站在兩側，則不同的安排方法有（　　）
A．232種 B．464種 C．288種 D．576種
組卷：33引用：1難度：0.5
解析
6．若圓C₁：（x-1）²+y²=1與圓C₂：x²+y²-8x+8y+m=0相切，則m的值可以是（　　）
A．16或-4 B．7或-7 C．7或-4 D．16或-7
組卷：34引用：4難度：0.8
解析
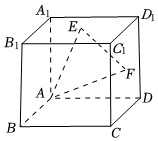7．已知正方體ABCD-A₁B₁C₁D₁的棱長為2，E，F分別為上底面A₁B₁C₁D₁和側面CDD₁C₁的中心，則點C到平面AEF的距離為（　　）
A．
4
11
11
B．
11
4
C．
11
11
D．
2
11
11
組卷：145引用：4難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本大題共6小題，共70分）

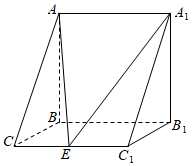21．如圖，三棱柱ABC-A₁B₁C₁中，AB⊥側面BB₁C₁C，已知
∠
BC
C
1
=
π
3
，BC=1，AB=C₁C=2，點E是棱C₁C的中點．
（1）求證：C₁B⊥平面ABC；
（2）求二面角A-EB₁-A₁的余弦值；
（3）在棱CA上是否存在一點M，使得EM與平面A₁B₁E所成角的正弦值為
2
11
11
，若存在，求出
CM
CA
的值；若不存在，請說明理由．
組卷：669引用：17難度：0.5
解析
22．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，四點
P
1
（
1
，
1
）
，
P
2
（
0
，
1
）
，
P
3
（
-
1
，
3
2
）
，
P
4
（
1
，
3
2
）
中恰有三點在橢圓C上．
（1）求橢圓C的標準方程；
（2）點P是橢圓C的上頂點，點Q，R在橢圓C上，若直線PQ，PR的斜率分別為k₁，k₂，滿足
k
1
?
k
2
=
3
4
，求△PQR面積的最大值．
組卷：87引用：5難度：0.5
解析