2023-2024學(xué)年山西省大同市、陽泉市多校九年級（上）聯(lián)考數(shù)學(xué)試卷（9月份）

一、選擇題（本大題共10個(gè)小題，每小題3分，共30分.在每個(gè)小題

• 1．一元二次方程x²-3=0的解為（　　）

  A．x1=x2= 3

  B．x1= 3 ，x2=- 3

  C．x1=x2=9

  D．x1=9，x2=-9
  組卷：47引用：2難度：0.7

  解析

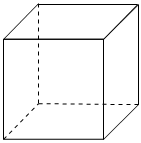• 2．如圖，一個(gè)正方體的棱長為x cm,它的表面積為y cm²，則y與x的函數(shù)關(guān)系式為（　　）

  A．y=x2

  B．y=3x2

  C．y=6x2

  D．y=12x2
  組卷：341引用：2難度：0.5

  解析

• 3．將一元二次方程x（x+1）=4化為一般形式后，它的各項(xiàng)系數(shù)的和為（　　）

  A．6

  B．4

  C．2

  D．-2
  組卷：49引用：2難度：0.7

  解析

• 4．二次函數(shù)y=x²+8x+9的對稱軸為直線（　　）

  A．x=4

  B．x=-4

  C． x = - 1 4

  D． x = 1 4
  組卷：299引用：3難度：0.6

  解析

• 5．我們解一元二次方程（x-3）²-5（x-3）=0時(shí)，可以運(yùn)用因式分解法將此方程化為（x-3）（x-3-5）=0．從而得到兩個(gè)一元一次方程：x-3=0或x-8=0．進(jìn)而得到原方程的解為x₁=3，x₂=8，這種解法體現(xiàn)的數(shù)學(xué)思想是（　　）

  A．?dāng)?shù)形結(jié)合思想	B．函數(shù)思想
  C．公理化思想	D．轉(zhuǎn)化思想
  組卷：41引用：1難度：0.7

  解析

• 6．一元二次方程x²-6x+1=0根的情況為（　　）

  A．有兩個(gè)不相等的實(shí)數(shù)根	B．有兩個(gè)相等的實(shí)數(shù)根
  C．沒有實(shí)數(shù)根	D．無法判斷其根的情況
  組卷：78引用：2難度：0.5

  解析

• 7．將拋物線y=x²-2向右平移3個(gè)單位長度，再向下平移1個(gè)單位長度，得到的拋物線的解析式為（　　）

  A．y=（x+3）2-3

  B．y=（x+3）2+3

  C．y=（x-3）2+3

  D．y=（x-3）2-3
  組卷：156引用：2難度：0.5

  解析

三、解答題（本大題共8個(gè)小題，共75分.解答應(yīng)寫出文字說明，證明過程或演算步驟）

• 22．綜合與實(shí)踐
  【項(xiàng)目學(xué)習(xí)】
  配方法是數(shù)學(xué)中重要的一種思想方法，利用配方法可求一元二次方程的根，也可以求二次函數(shù)的頂點(diǎn)坐標(biāo)等．所謂配方法是指將一個(gè)式子的某部分通過恒等變形化為完全平方式或幾個(gè)完全平方式的和的方法．其實(shí)這種方法還經(jīng)常被用到代數(shù)式的變形中，并結(jié)合非負(fù)數(shù)的意義解決某些問題．
  例1：把代數(shù)式x²+8x+25進(jìn)行配方．
  解：原式=x²+8x+16+9=（x+4）²+9．
  例2：求代數(shù)式-x²+4x-7的最大值．
  解：原式=-（x²-4x+4）-3=-（x-2）²-3．∵（x-2）²≥0，∴-（x-2）²≤0，∴-（x-2）²-3≤-3，∴-x²+4x-7的最大值為-3．
  【問題解決】
  （1）若m,k,h滿足2m²-12m+11=2（m-k）²+h,求k+h的值．
  （2）若等腰△ABC的三邊長a,b,c均為整數(shù)，且滿足a²+2b²-8a-20b=-66，求△ABC的周長．
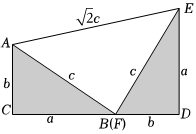
  （3）如圖，這是美國總統(tǒng)加菲爾德證明勾股定理的一個(gè)圖形，其中a,b,c是Rt△ABC和Rt△DEF的三邊長，根據(jù)勾股定理可得AE=

  c

  2

  +

  c

  2

  =

  2

  c,我們把關(guān)于x的一元二次方程ax²+

  2

  cx+b=0稱為“勾系一元二次方程”．已知實(shí)數(shù)p,q滿足等式q-p²+15p-48=0，且p+q的最小值是“勾系一元二次方程”ax²+

  2

  cx+b=0的一個(gè)根．四邊形ACDE的周長為6

  2

  ，試求△ABC的面積．
  組卷：230引用：1難度：0.7

  解析

• 23．綜合與探究
  如圖1，已知拋物線y=x²+bx+c與x軸相交于點(diǎn)A（-3，0），B（1，0），與y軸交于點(diǎn)C．
  （1）求拋物線y=x²+bx+c及直線AC的函數(shù)表達(dá)式．
  （2）如圖2，P是直線AC下方的拋物線上的一點(diǎn)，過點(diǎn)P作PQ⊥x軸于點(diǎn)Q，交直線AC于點(diǎn)D，當(dāng)

  S

  △

  CQD

  S

  △

  CPD

  =

  1

  2

  時(shí)，求點(diǎn)P的坐標(biāo)．
  （3）如圖3，過點(diǎn)O作OM⊥AC于點(diǎn)M，將線段OM所在的直線沿著x軸平移，使得平移后的直線交x軸于點(diǎn)E，交拋物線于點(diǎn)F，是否存在點(diǎn)F，使得四邊形OMEF是平行四邊形？若存在，直接寫出點(diǎn)F的坐標(biāo)；若不存在，請說明理由．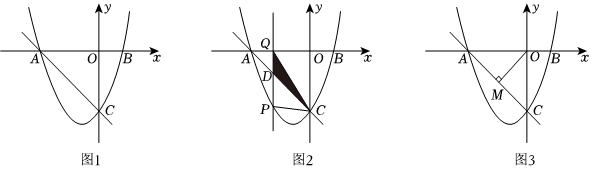
  組卷：99引用：1難度：0.3

  解析