2022-2023學年河北省唐山市高三（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合

  A

  =

  {

  x

  |

  1

  x

  ≥

  1

  }

  ，

  B

  =

  {

  x

  |

  y

  =

  lo

  g

  2

  （

  1

  -

  x

  ）

  }

  ，則A∩B=（　　）

  A．（0，1）

  B．（0，1]

  C．（-∞，1）

  D．（-∞，1]
  組卷：65引用：3難度：0.8

  解析

• 2．已知函數

  f

  （

  x

  ）

  =

  2

  x

  x

  2

  +

  1

  ，則其圖像大致為（　　）

  A．

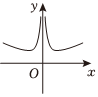
  B．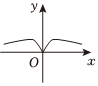

  C．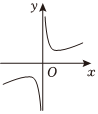

  D．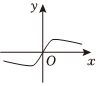
  組卷：68引用：2難度：0.8

  解析

• 3．已知函數

  f

  （

  x

  ）

  =

  3

  sin

  2

  x

  -

  cos

  2

  x

  ，則（　　）

  A．f（x）在 （ - π 6 ， 0 ） 單調遞增，且圖象關于直線 x = π 6 對稱

  B．f（x）在 （ - π 6 ， 0 ） 單調遞增，且圖象關于直線 x = π 3 對稱

  C．f（x）在 （ - π 6 ， 0 ） 單調遞減，且圖象關于直線 x = π 6 對稱

  D．f（x）在 （ - π 6 ， 0 ） 單調遞減，且圖象關于直線 x = π 3 對稱
  組卷：367引用：3難度：0.7

  解析

• 4．

  （

  x

  -

  a

  x

  ）

  n

  的展開式共有七項，且常數項為20，則a=（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：258引用：3難度：0.8

  解析

• 5．直線l：x-y-1=0與拋物線C：y²=4x交于A，B兩點，則|AB|=（　　）

  A．8

  B． 4 2

  C．4

  D． 2 2
  組卷：66引用：2難度：0.7

  解析

• 6．高斯（Gauss）被認為是歷史上最重要的數學家之一，并享有“數學王子”之稱．小學進行1+2+3+?+100的求和運算時，他是這樣算的：1+100=101，2+99=101，?，50+51=101，共有50組，所以50×101=5050，這就是著名的高斯法，又稱為倒序相加法．事實上，高斯發現并利用了等差數列的對稱性．若函數y=f（x）的圖象關于點

  （

  1

  2

  ，

  1

  ）

  對稱，

  S

  n

  =

  （

  n

  +

  1

  ）

  [

  f

  （

  1

  n

  +

  1

  ）

  +

  f

  （

  2

  n

  +

  1

  ）

  +

  ?

  +

  f

  （

  n

  n

  +

  1

  ）

  ]

  ，

  S

  n

  為數列{a_n}的前n項和，則下列結論中，錯誤的是（　　）

  A．f（x）+f（1-x）=2	B．Sn=n（n+1）
  C． S n = n （ 1 + a n ） 2	D． 1 S 1 + 1 S 2 + 1 S 3 + ? + 1 S n ＜ 1
  組卷：122引用：2難度：0.5

  解析

• 7．已知正三棱錐P-ABC的側棱長為2，則該三棱錐體積最大時，其外接球的表面積為（　　）

  A．8π

  B．10π

  C．12π

  D．14π
  組卷：196引用：2難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知橢圓E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  2

  2

  ，點

  P

  （

  1

  ，

  2

  2

  ）

  在E上，不經過點P的直線l：y=kx+m與E交于不同的兩點A，B．
  （1）求E的方程；
  （2）若直線PA與直線PB的斜率之和為0，求k的值及m的取值范圍．
  組卷：58引用：2難度：0.5

  解析

• 22．已知函數f（x）=（e^x-1）x,g（x）=f（x）-a.
  （1）求f（x）的極值；
  （2）若a＞0，證明：函數g（x）有兩個零點x₁，x₂，且x₁+x₂＜0．
  組卷：138引用：1難度：0.3

  解析