當前位置：試卷中心 > 試卷詳情

2011-2012學年江蘇省常州市奔牛高級中學高二（上）數學寒假作業3（理科）

發布：2024/12/24 3:0:2

1．過定點F（1，0）且與直線x=-1相切的動圓圓心M的軌跡方程為
．
組卷：231引用：9難度：0.5
解析
2．在空間直角坐標系O-xyz中，點P（2，1，3）關于平面xoy的對稱點坐標為
．
組卷：25引用：3難度：0.9
解析
3．已知方程
x
2
2
-
k
+
y
2
k
-
1
=
1
表示雙曲線，則實數k的取值范圍是
．
組卷：64引用：6難度：0.7
解析
4．若施化肥量x與小麥產量y之間的回歸方程為
?
y
=250+4x（單位：kg），當施化肥量為50kg時，預計小麥產量為
kg.
組卷：210引用：4難度：0.9
解析
5．在平面上，若兩個正三角形的邊長的比為1：2，則它們的面積比為1：4，類似地，在空間內，若兩個正四面體的棱長的比為1：2，則它們的體積比為
．
組卷：544引用：54難度：0.7
解析
6．已知命題p：直線a與平面α內無數條直線垂直，q：直線a與平面α垂直．則p是q的
條件．
（填“充分不必要，必要不充分，充要，既不充分又不必要”之一）
組卷：25引用：5難度：0.7
解析

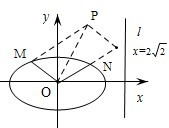19．如圖，橢圓的中心為原點O，離心率e=
2
2
，一條準線的方程為x=2
2
．
（Ⅰ）求該橢圓的標準方程．
（Ⅱ）設動點P滿足
OP
=
OM
+
2
ON
，其中M，N是橢圓上的點．直線OM與ON的斜率之積為-
1
2
．
問：是否存在兩個定點F₁，F₂，使得|PF₁|+|PF₂|為定值．若存在，求F₁，F₂的坐標；若不存在，說明理由．
組卷：1940引用：5難度：0.5
解析
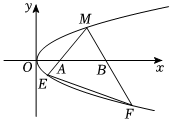20．如圖，M是拋物線上y²=x上的一點，動弦ME、MF分別交x軸于A、B兩點，且MA=MB．
（1）若M為定點，證明：直線EF的斜率為定值；
（2）若M為動點，且∠EMF=90°，求△EMF的重心G的軌跡方程．
組卷：1568引用：11難度：0.5
解析