人教新版九年級下冊《27.2 相似三角形》2021年同步練習卷(廣東省潮州市饒平縣英才實驗中學)(1)
發布:2024/4/20 14:35:0
一.選擇題(共12小題)
-
1.在某一時刻,測得一根高為1.8m的竹竿的影長為3m,同時測得一根旗桿的影長為25m,那么這根旗桿的高度為( )
A.10m B.12m C.15m D.40m 組卷:1159引用:19難度:0.9 -
 2.如圖,為了估計河的寬度,在河的對岸選定一個目標點P,在近岸取點Q和S,使點P,Q,S在一條直線上,且直線PS與河垂直,在過點S且與PS垂直的直線a上選擇適當的點T,PT與過點Q且與PS垂直的直線b的交點為R.如果QS=60m,ST=120m,QR=80m,則河的寬度PQ為( )
2.如圖,為了估計河的寬度,在河的對岸選定一個目標點P,在近岸取點Q和S,使點P,Q,S在一條直線上,且直線PS與河垂直,在過點S且與PS垂直的直線a上選擇適當的點T,PT與過點Q且與PS垂直的直線b的交點為R.如果QS=60m,ST=120m,QR=80m,則河的寬度PQ為( )A.40m B.60m C.120m D.180m 組卷:2202引用:14難度:0.9 -
3.如圖,是小孔成像原理的示意圖,根據圖所標注的尺寸,這支蠟燭在暗盒中所成的像CD的長是( )
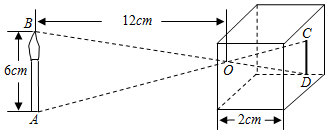
A. 16cmB. 13cmC. 12cmD.1cm 組卷:722引用:19難度:0.9 -
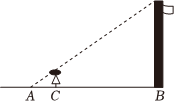 4.如圖,為估算學校的旗桿的高度,身高1.6米的小紅同學沿著旗桿在地面的影子AB由A向B走去,當她走到點C處時,她的影子的頂端正好與旗桿的影子的頂端重合,此時測得AC=2m,BC=8m,則旗桿的高度是( )
4.如圖,為估算學校的旗桿的高度,身高1.6米的小紅同學沿著旗桿在地面的影子AB由A向B走去,當她走到點C處時,她的影子的頂端正好與旗桿的影子的頂端重合,此時測得AC=2m,BC=8m,則旗桿的高度是( )A.6.4m B.7m C.8m D.9m 組卷:1819引用:27難度:0.9 -
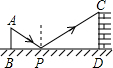 5.如圖是小明測量某古城墻高度的示意圖,點P處放一水平的平面鏡,然后,后退至點B,從點A經平面鏡剛好看到古城墻CD的頂端C處,已知AB⊥BD,CD⊥BD,且測得AB=1.2米,BP=1.8米,PD=12米,那么該古城墻的高度是( )
5.如圖是小明測量某古城墻高度的示意圖,點P處放一水平的平面鏡,然后,后退至點B,從點A經平面鏡剛好看到古城墻CD的頂端C處,已知AB⊥BD,CD⊥BD,且測得AB=1.2米,BP=1.8米,PD=12米,那么該古城墻的高度是( )A.6米 B.8米 C.18米 D.24米 組卷:475引用:4難度:0.9 -
 6.學校門口的欄桿如圖所示,欄桿從水平位置BD繞O點旋轉到AC位置,已知AB⊥BD,CD⊥BD,垂足分別為B,D,AO=4m,AB=1.6m,CO=1m,則欄桿C端應下降的垂直距離CD為( )
6.學校門口的欄桿如圖所示,欄桿從水平位置BD繞O點旋轉到AC位置,已知AB⊥BD,CD⊥BD,垂足分別為B,D,AO=4m,AB=1.6m,CO=1m,則欄桿C端應下降的垂直距離CD為( )A.0.2m B.0.3m C.0.4m D.0.5m 組卷:3268引用:39難度:0.7 -
 7.如圖,四邊形ABCD和四邊形A′B′C′D′是以點O為位似中心的位似圖形,若OA:OA′=2:3,四邊形ABCD的面積等于4,則四邊形A′B′C′D′的面積為( )
7.如圖,四邊形ABCD和四邊形A′B′C′D′是以點O為位似中心的位似圖形,若OA:OA′=2:3,四邊形ABCD的面積等于4,則四邊形A′B′C′D′的面積為( )A.3 B.4 C.6 D.9 組卷:1240引用:14難度:0.8 -
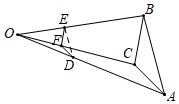 8.如圖,已知△ABC,在△ABC外任取一點O,連結AO、BO、CO,在線段AO、BO、CO上分別取點D、E、F,使OD=AO,OE=13BO,OF=13CO,得△DEF,有下列說法:13
8.如圖,已知△ABC,在△ABC外任取一點O,連結AO、BO、CO,在線段AO、BO、CO上分別取點D、E、F,使OD=AO,OE=13BO,OF=13CO,得△DEF,有下列說法:13
①△ABC與△DEF是位似圖形;
②△ABC與△DEF是相似圖形;
③△DEF與△ABC的周長比為1:3;
④△DEF與△ABC的面積比為1:6.
則正確的個數是( )A.1 B.2 C.3 D.4 組卷:726引用:5難度:0.8 -
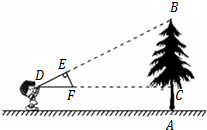 9.如圖,小明同學用自制的直角三角形紙板DEF測量樹的高度AB,他調整自己的位置,設法使斜邊DF保持水平,并且邊DE與點B在同一直線上.已知紙板的兩條直角邊DE=40cm,EF=20cm,測得邊DF離地面的高度AC=1.5m,CD=8m,則樹高AB是( )
9.如圖,小明同學用自制的直角三角形紙板DEF測量樹的高度AB,他調整自己的位置,設法使斜邊DF保持水平,并且邊DE與點B在同一直線上.已知紙板的兩條直角邊DE=40cm,EF=20cm,測得邊DF離地面的高度AC=1.5m,CD=8m,則樹高AB是( )A.4米 B.4.5米 C.5米 D.5.5米 組卷:3497引用:24難度:0.7
三.解答題(共8小題)
-
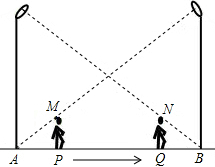 28.如圖,小華在晚上由路燈A走向路燈B.當他走到點P時,發現他身后影子的頂部剛好接觸到路燈A的底部;當他向前再步行12m到達點Q時,發現他身前影子的頂部剛好接觸到路燈B的底部.已知小華的身高是1.6m,兩個路燈的高度都是9.6m,且AP=QB.
28.如圖,小華在晚上由路燈A走向路燈B.當他走到點P時,發現他身后影子的頂部剛好接觸到路燈A的底部;當他向前再步行12m到達點Q時,發現他身前影子的頂部剛好接觸到路燈B的底部.已知小華的身高是1.6m,兩個路燈的高度都是9.6m,且AP=QB.
(1)求兩個路燈之間的距離.
(2)當小華走到路燈B的底部時,他在路燈A下的影長是多少?組卷:5034引用:11難度:0.3 -
29.在△ABC中,∠B=90°,AB=6cm,BC=12cm,點P從點A開始沿AB邊向點B以1cm/s的速度移動,點Q從點B開
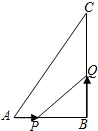 始沿BC邊向點C以2cm/s的速度移動,設P、Q兩點同時出發,移動時間為t秒.
始沿BC邊向點C以2cm/s的速度移動,設P、Q兩點同時出發,移動時間為t秒.
(1)幾秒鐘后△PBQ是等腰三角形?
(2)幾秒鐘后△PQB的面積為5cm2?
(3)幾秒鐘后,以P、B、Q為頂點的三角形和△ABC相似?組卷:2219引用:4難度:0.3


