2022-2023學(xué)年廣東省深圳高級(jí)中學(xué)高中園高一（下）期中數(shù)學(xué)試卷

一、單項(xiàng)選擇題：（本題共8小題，每小題滿分40分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)符合題目要求，選對(duì)得5分，選錯(cuò)得0分）

• 1．已知復(fù)數(shù)z=

  1

  +

  i

  i

  ，則|z|是（　　）

  A．1

  B． 2

  C．2

  D． 3
  組卷：94引用：6難度：0.9

  解析

• 2．已知向量

  a

  =（1，2），

  b

  =（-2，t），若

  a

  ∥

  b

  ，則t=（　　）

  A．-4

  B．1

  C．2

  D．4
  組卷：847引用：17難度：0.8

  解析

• 3．已知圓錐軸截面為正三角形，母線長(zhǎng)為2，則該圓錐的體積等于（　　）

  A． 3 3 π

  B． 3 π

  C． 2 3 π

  D．2π
  組卷：430引用：9難度：0.9

  解析

• 4．用斜二測(cè)畫法作出一個(gè)三角形的直觀圖，則原三角形面積是直觀圖面積的（　　）

  A． 1 2 倍

  B．2 2 倍

  C．2倍

  D． 2 4 倍
  組卷：462引用：6難度：0.7

  解析

• 5．已知

  cosα

  +

  cosβ

  =

  1

  2

  ，

  sinα

  -

  sinβ

  =

  1

  3

  ，則cos（α+β）的值為（　　）

  A． - 13 72

  B． 13 72

  C． - 59 72

  D． 59 72
  組卷：800引用：6難度：0.6

  解析

• 6．在△ABC中，

  AN

  =

  1

  4

  NC

  ，P是直線BN上的一點(diǎn)，若

  AP

  =m

  AB

  +

  2

  5

  AC

  ，則實(shí)數(shù)m的值為（　　）

  A．-4

  B．-1

  C．1

  D．4
  組卷：466引用：7難度：0.7

  解析

• 7．已知△ABC的外接圓圓心O，且

  2

  AO

  =

  AB

  +

  AC

  ，

  |

  OA

  |

  =

  |

  AB

  |

  ，則向量

  BA

  在向量

  BC

  上的投影向量為（　　）

  A． 1 4 BC

  B． 3 4 BC

  C．- 1 4 BC

  D．- 3 4 BC
  組卷：706引用：24難度：0.8

  解析

四、解答題：（本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟）

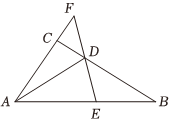• 21．如圖所示，在△ABC中，D為BC邊上一點(diǎn)，且

  BD

  =

  2

  DC

  ，過D的直線EF與直線AB相交于E點(diǎn)，與直線AC相交于F點(diǎn)（E，F(xiàn)兩點(diǎn)不重合）．
  （1）用

  AB

  ，

  AC

  表示

  AD

  ；
  （2）若

  AE

  =

  λ

  AB

  ，

  AF

  =

  μ

  AC

  ，求2λ+μ的最小值．
  組卷：606引用：5難度：0.5

  解析

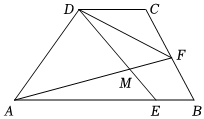• 22．如圖，在梯形ABCD中，AB∥CD，AB=5，AD=2DC=4，且

  AC

  ?

  BD

  =

  0

  ，E是線段AB上一點(diǎn)，且AE=4EB，F(xiàn)為線段BC上一動(dòng)點(diǎn)．
  （1）求∠DAB的大小；
  （2）若F為線段BC的中點(diǎn)，直線AF與DE相交于點(diǎn)M，求cos∠EMF；
  （3）求

  AF

  ?

  DF

  的取值范圍．
  組卷：215引用：5難度：0.5

  解析