2023-2024學年江蘇省宿遷市宿城區八年級（上）期中數學試卷
發布：2024/10/24 14:0:2
一、選擇題（本大題共8小題，每小題3分，共24分.在每小題給出的四個選項中，有
-
1．在以下綠色食品、回收、節能、節水四個標志中，是軸對稱圖形的是（ ）
組卷：223引用：11難度：0.8 -
2．滿足下列條件時，△ABC不是直角三角形的是（ ）
組卷：195引用：2難度：0.7 -
3．如圖，點C在∠AOB的OB邊上，用尺規作出了CN∥OA，連接EN，作圖痕跡中，△ODM≌△CEN根據的是（ ）組卷：855引用：8難度：0.7 -
4．若等腰三角形有一個內角為110°，則這個等腰三角形的底角是（ ）
組卷：1467引用：18難度：0.7 -
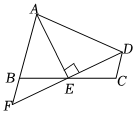5．如圖，在四邊形ABCD中，AB∥DC，E為BC的中點，連接DE，AE，AE⊥DE，延長DE交AB的延長線于點F．若AB=5，CD=2，則AD的長為（ ）組卷：180引用：7難度：0.5 -
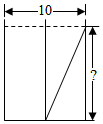6．我國古代數學著作《九章算術》中記載了一個問題：“今有池方一丈，葭（jiā）生其中，出水一尺．引葭赴岸，適與岸齊．問水深幾何．”（丈、尺是長度單位，1丈=10尺）其大意為：有一個水池，水面是一個邊長為10尺的正方形，在水池正中央有一根蘆葦，它高出水面1尺．如果把這根蘆葦拉向水池一邊的中點，它的頂端恰好到達池邊的水面．水的深度是多少？則水深為（ ）組卷：1368引用：12難度：0.5 -
7．已知，如圖，長方形ABCD中，AB=3cm,AD=9cm,將此長方形折疊，使點B與點D重合，折痕為EF，則△ABE的面積為（ ）組卷：1028引用：24難度：0.7 -
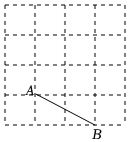8．在正方形網格中每個小正方形的邊長都是1，已知線段AB，以AB為腰畫等腰△ABC，則頂點C共有（ ）組卷：353引用：5難度：0.4
二、填空題.（本大題共10小題，每小題3分，共30分.不需寫出解答過程，請把答案
-
9．如圖是從鏡子里看到的號碼，則實際號碼應是 ．組卷：996引用：16難度：0.5
三、解答題（本大題共10題，共96分.解答時應寫出必要的文字說明、證明過程或演算
-
27．【探索發現】
如圖①，已知在△ABC中，∠BAC=45°，AD⊥BC，垂足為D，BE⊥AC，垂足為E，AD與BE相交于F．
（1）線段AF與BC的數量關系是：AF BC（用＞，＜，=填空）；
（2）若∠ABC=67.5°，試猜想線段AF與BD有何數量關系，并說明理由；
【拓展應用】
（3）如圖②，在△ABC中，AD⊥BC，垂足為D，已知∠BAC=45°，∠C=22.5°，AD=3，求△ABC的面積．組卷：61引用：1難度：0.1 -
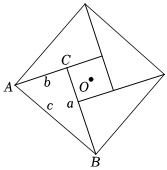28．在Rt△ABC中，∠ACB=90°，BC=a,AC=b,AB=c.將Rt△ABC繞點O依次旋轉90°、180°和270°，構成的圖形如圖所示．該圖是我國古代數學家趙爽制作的“勾股圓方圖”，也被稱作“趙爽弦圖”，它是我國最早對勾股定理證明的記載，也成為了2002年在北京召開的國際數學家大會的會標設計的主要依據．
（1）請利用這個圖形證明勾股定理；
（2）請利用這個圖形說明a2+b2≥2ab,并說明等號成立的條件；
（3）請根據（2）的結論解決下面的問題：長為x,寬為y的長方形，其周長為8，求當x,y取何值時，該長方形的面積最大？最大面積是多少？組卷：573引用：4難度：0.2