2022年北京市順義二中高考數學適應性試卷

一、選擇題共10小題，每小題4分，共40分。在每小題列出的四個選項中，選出符合題目要求的一項。

• 1．已知集合U=R，A={x|x²-2x-3＜0}，則?_UA=（　　）

  A．{x|-1＜x＜3}

  B．{x|-1≤x≤3}

  C．{x|x≤-1或x≥3}

  D．{x|x＜-1或x＞3}
  組卷：305引用：3難度：0.7

  解析

• 2．已知復數z滿足z（1-3i）=2+i,則|z|=（　　）

  A． 2 2

  B． 3 2

  C． 2

  D． 2 2
  組卷：157引用：2難度：0.8

  解析

• 3．若等差數列{a_n}和等比數列{b_n}滿足a₁=b₁=-1，a₄=b₄=8，

  a

  2

  b

  2

  =（　　）

  A．-4

  B．-1

  C．1

  D．4
  組卷：402引用：14難度：0.7

  解析

• 4．若

  a

  =

  2

  1

  3

  ，b=log_π3，c=

  lo

  g

  2

  1

  3

  ，則（　　）

  A．c＜b＜a

  B．c＜a＜b

  C．b＜a＜c

  D．a＜b＜c
  組卷：513引用：4難度：0.8

  解析

• 5．若非零實數a,b滿足a＞b,則下列不等式一定成立的是（　　）

  A． 1 a ＞ 1 b

  B．a+b＞2 ab

  C．lga2＞lgb2

  D．a3＞b3
  組卷：323引用：7難度：0.8

  解析

• 6．已知lga+lgb=0（a＞0且a≠1，b＞0且b≠1），則函數f（x）=a^x與

  g

  （

  x

  ）

  =

  lo

  g

  1

  b

  x

  的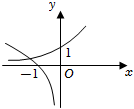圖象可能是（　　）

  A．

  B．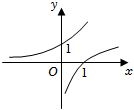

  C．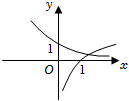

  D．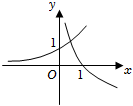
  組卷：229引用：4難度：0.7

  解析

• 7．已知P（x₀，2）為拋物線C：y²=2px（p＞0）上一點，點P到拋物線C的焦點的距離與它到y軸的距離之比為3：2，則p=（　　）

  A． 2

  B．2

  C． 2 2

  D．3
  組卷：309引用：4難度：0.7

  解析

三、解答題共6小題，共85分.解答應寫出文字說明，演算步驟或證明過程.

• 20．已知函數f（x）=alnx+

  1

  x

  （a∈R）．
  （1）若a=2，求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）求f（x）的極值和單調區間；
  （3）若f（x）在[1，e]上不是單調函數，且f（x）≤e在[1，e]上恒成立，求實數a的取值范圍．
  組卷：443引用：2難度：0.4

  解析

• 21．對于項數為m（m＞1）的有窮正整數數列{a_n}，記b_k=max{a₁，a₂，…，a_k}（k=1，2，…，m），即b_k為a₁，a₂，…a_k中的最大值，稱數列{b_n}為數列{a_n}的“創新數列”．比如1，3，2，5，5的“創新數列”為1，3，3，5，5．
  （Ⅰ）若數列{a_n}的“創新數列”{b_n}為1，2，3，4，4，寫出所有可能的數列{a_n}；
  （Ⅱ）設數列{b_n}為數列{a_n}的“創新數列”，滿足a_k+b_m-k+1=2018（k=1，2，…，m），求證：a_k=b_k（k=1，2，…，m）；
  （Ⅲ）設數列{b_n}為數列{a_n}的“創新數列”，數列{b_n}中的項互不相等且所有項的和等于所有項的積，求出所有的數列{a_n}．
  組卷：211引用：5難度：0.3

  解析