2023-2024學年山東省青島實驗高中高二（上）期中數學試卷

一、單選題（本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，

• 1．直線

  x

  -

  3

  y

  +

  1

  =

  0

  的傾斜角為（　　）

  A． 2 π 3

  B． 5 π 6

  C． π 3

  D． π 6
  組卷：625引用：20難度：0.9

  解析

• 2．雙曲線2x²-y²=8的漸近線方程是（　　）

  A． y =± 1 2 x

  B．y=±2x

  C． y =± 2 x

  D． y =± 2 2 x
  組卷：375引用：6難度：0.8

  解析

• 3．直線

  x

  4

  +

  y

  2

  =1與x軸，y軸分別交于點A，B，以線段AB為直徑的圓的方程為（　　）

  A．x2+y2-4x-2y-1=0	B．x2+y2-4x-2y=0
  C．x2+y2-4x-2y+1=0	D．x2+y2-2x-4y=0
  組卷：205引用：6難度：0.7

  解析

• 4．已知隨機事件A和B互斥，且P（A∪B）=0.6，P（B）=0.3，則

  P

  （

  A

  ）

  等于（　　）

  A．0.8

  B．0.7

  C．0.5

  D．0.2
  組卷：286引用：11難度：0.7

  解析

• 5．圓x²+y²+4x-2y=0和圓x²+y²-2x-3=0交于A、B兩點，則相交弦AB的垂直平分線的方程為（　　）

  A．6x-2y+3=0

  B．x+3y-1=0

  C．2x-2y+3=0

  D．x-3y-1=0
  組卷：974引用：5難度：0.8

  解析

• 6．已知△ABC的周長為20，且頂點B（0，-4），C（0，4），則頂點A的軌跡方程是（　　）

  A． x 2 36 + y 2 20 = 1 （x≠0）	B． x 2 20 + y 2 36 = 1 （x≠0）
  C． x 2 6 + y 2 20 = 1 （x≠0）	D． x 2 20 + y 2 6 = 1 （x≠0）
  組卷：10606引用：56難度：0.9

  解析

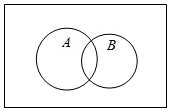• 7．已知一個古典概型的樣本空間Ω和事件A，B如圖所示．其中n（Ω）=12，n（A）=6，n（B）=4，n（A∪B）=8，則事件A與事件

  B

  （　　）

  A．是互斥事件，不是獨立事件

  B．不是互斥事件，是獨立事件

  C．既是互斥事件，也是獨立事件

  D．既不是互斥事件，也不是獨立事件
  組卷：1009引用：7難度：0.9

  解析

四、解答題（本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.除17題為10分外，18～22題均為12分.）

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右焦點分別為F₁，F₂（|F₁F₂|＜10），上頂點為A，AF₁⊥AF₂，且F₁到直線l：

  x

  -

  2

  y

  +

  5

  =

  0

  的距離為

  4

  3

  3

  ．
  （1）求C的方程；
  （2）與l平行的一組直線與C相交時，證明：這些直線被C截得的線段的中點在同一條直線上；
  （3）P為C上的動點，M，N為l上的動點，且

  |

  MN

  |

  =

  2

  3

  ，求△PMN面積的取值范圍．
  組卷：123引用：5難度：0.5

  解析

• 22．杭州2022年第19屆亞運會（The19thAsianGamesHangzhou2022）將于2023年9月23日至10月8日舉辦．本屆亞運會共設40個競賽大項，包括31個奧運項目和9個非奧運項目．同時，在保持40個大項目不變的前提下，增設了霹靂舞、電子競技兩個競賽項目．與傳統的淘汰賽不同，近年來一個新型的賽制“雙敗賽制”贏得了許多賽事的青睞．傳統的淘汰賽失敗一場就喪失了冠軍爭奪的權利，而在雙敗賽制下，每人或者每個隊伍只有失敗了兩場才會淘汰出局，因此更有容錯率．假設最終進入到半決賽有四支隊伍，淘汰賽制下會將他們四支隊伍兩兩分組進行比賽，勝者進入到總決賽，總決賽的勝者即為最終的冠軍．雙敗賽制下，兩兩分組，勝者進入到勝者組，敗者進入到敗者組，勝者組兩個隊伍對決的勝者將進入到總決賽，敗者進入到敗者組．之前進入到敗者組的兩個隊伍對決的敗者將直接淘汰，勝者將跟勝者組的敗者對決，其中的勝者進入總決賽，最后總決賽的勝者即為冠軍．雙敗賽制下會發生一個有意思的事情，在勝者組中的勝者只要輸一場比賽即總決賽就無法拿到冠軍，但是其它的隊伍卻有一次失敗的機會，近年來從敗者組殺上來拿到冠軍的不在少數，因此很多人戲謔這個賽制對強者不公平，是否真的如此呢？這里我們簡單研究一下兩個賽制：假設四支隊伍分別為A，B，C，D，其中A對陣其他三個隊伍獲勝概率均為p,另外三支隊伍彼此之間對陣時獲勝概率均為

  1

  2

  ．最初分組時AB同組，CD同組．
  
  （1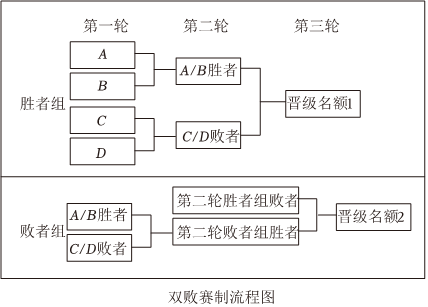）若

  p

  =

  3

  4

  ，在淘汰賽賽制下，A，C獲得冠軍的概率分別為多少？
  （2）分別計算兩種賽制下A獲得冠軍的概率（用p表示），并據此簡單分析一下雙敗賽制下對隊伍的影響，是否如很多人質疑的“對強者不公平”？
  組卷：184引用：9難度：0.6

  解析