2022-2023學年江西省撫州市黎川二中高一（下）期末數學試卷

一、單選題（每題5分，共40分）

• 1．復數（1+2i）-（3-4i）對應的點在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：29引用：2難度：0.7

  解析

• 2．已知向量

  a

  =（1，2），

  b

  =（-2，m），若

  a

  與

  b

  共線，則實數m=（　　）

  A．1

  B．-1

  C．4

  D．-4
  組卷：39引用：2難度：0.9

  解析

• 3．在△ABC中，若AD為BC邊上的中線，點E在AD上，且AE=2ED，則

  EB

  =（　　）

  A． 2 3 AB - 1 3 AC

  B． 2 3 AC - 1 3 AB

  C． 7 6 AB - 5 6 AC

  D． 7 6 AC - 5 6 AB
  組卷：375引用：15難度：0.8

  解析

• 4．已知直角梯形OABC上下兩底分別為分別為2和4，高為

  2

  2

  ，則利用斜二測畫法所得其直觀圖的面積為（　　）

  A． 6 2

  B． 3 2

  C．3

  D．6
  組卷：1173引用：8難度：0.8

  解析

• 5．設f（α）=

  2

  sin

  （

  2

  π

  -

  α

  ）

  cos

  （

  2

  π

  +

  α

  ）

  -

  cos

  （

  -

  α

  ）

  1

  +

  si

  n

  2

  α

  +

  sin

  （

  2

  π

  +

  α

  ）

  -

  co

  s

  2

  （

  4

  π

  -

  α

  ）

  ，則f（-

  23

  6

  π）的值為（　　）

  A． 3 3

  B．- 3 3

  C． 3

  D．- 3
  組卷：422引用：3難度：0.7

  解析

• 6．在△ABC中，已知a=

  3

  ，b=1，A=130°，則此三角形解的情況為（　　）

  A．無解	B．只有一解
  C．有兩解	D．解的個數不確定
  組卷：135引用：3難度：0.9

  解析

• 7．在四面體ABCD中，AB⊥平面

  BCD

  ，

  AB

  =

  CD

  =

  2

  ，

  BC

  =

  2

  ，

  ∠

  BCD

  =

  45

  °

  ，則點B到平面ACD的距離為（　　）

  A． 3 7 7

  B． 3 5 5

  C． 2 7 7

  D． 2 5 5
  組卷：49引用：3難度：0.5

  解析

四、解答題（共70分）

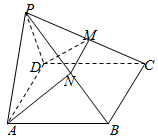• 21．如圖，在四棱錐P-ABCD中，底面ABCD為平行四邊形，N是PB中點，過A、N、D三點的平面交PC于M．求證：
  （1）PD∥平面ANC；
  （2）M是PC中點．
  組卷：928引用：5難度：0.3

  解析

• 22．已知函數f（x）=sin（

  ωx

  +

  π

  4

  ），g（x）=2sin（

  4

  3

  x

  -

  π

  3

  ）-1，且滿足?x∈[0，π]，f（x）?g（x）≤0恒成立．
  （1）求解g（x）的零點以及f（x）的函數解析式．
  （2）求函數f（x）在區間

  [

  t

  ,

  t

  +

  π

  4

  ]上最大值與最小值之差的取值范圍．
  組卷：67引用：2難度：0.4

  解析