蘇科新版八年級上冊《第1章 全等三角形》2021年單元測試卷(3)
發布:2024/11/18 11:30:1
一、選擇題。(每題3分,共21分)
-
1.下列各組中的兩個圖形屬于全等圖形的是( )
A. 
B. 
C. 
D.  組卷:2017引用:6難度:0.7
組卷:2017引用:6難度:0.7 -
2.如圖,已知△ABC的六個元素,則下列甲、乙、丙三個三角形中和△ABC全等的圖形是( )
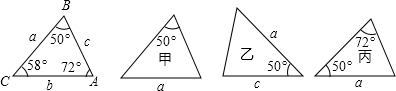
A.甲乙 B.甲丙 C.乙丙 D.乙 組卷:1049引用:83難度:0.9 -
3.已知△ABC≌△A′B′C′,∠A=80°,∠B=40°,那么∠C′的度數為( )
A.80° B.40° C.60° D.120° 組卷:400引用:11難度:0.9 -
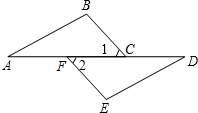 4.如圖,∠A=∠D,∠ACB=∠DFE.下列條件中,能使△ABC≌△DEF的是( )
4.如圖,∠A=∠D,∠ACB=∠DFE.下列條件中,能使△ABC≌△DEF的是( )A.∠E=∠B B.ED=BC C.AB=EF D.AF=CD 組卷:241引用:14難度:0.9 -
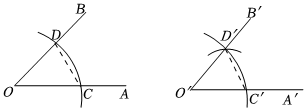 5.小聰在用直尺和圓規作一個角等于已知角時,具體過程是這樣的:
5.小聰在用直尺和圓規作一個角等于已知角時,具體過程是這樣的:
已知:∠AOB.
求作:∠A′O′B′,使∠A′O′B′=∠AOB.
作法:(1)如圖,以點O為圓心,任意長為半徑畫弧,分別交OA,OB于點C,D;
(2)畫一條射線O′A′,以點O′為圓心,OC長為半徑畫弧,交O′A′于點C′;
(3)以點C'為圓心,CD長為半徑畫弧,與第(2)步中所畫的弧相交于點D′;
(4)過點D'畫射線O′B′,則∠A′O′B′=∠AOB.
小聰作法正確的理由是( )A.由SSS可得△O′C′D′≌△OCD,進而可證∠A′O′B′=∠AOB B.由SAS可得△O′C′D′≌△OCD,進而可證∠A′O′B′=∠AOB C.由ASA可得△O′C′D′≌△OCD,進而可證∠A′O′B′=∠AOB D.由“等邊對等角”可得∠A′O′B′=∠AOB 組卷:726引用:16難度:0.7 -
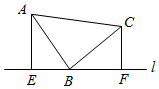 6.如圖所示,在等腰Rt△ABC中,∠ABC=90°,BA=BC=10,直線l過點B,分別過點A、C作直線l的垂線,垂足分別為E、F,若BE=8,AE=6,則CF的長為( )
6.如圖所示,在等腰Rt△ABC中,∠ABC=90°,BA=BC=10,直線l過點B,分別過點A、C作直線l的垂線,垂足分別為E、F,若BE=8,AE=6,則CF的長為( )A.5 B.6 C.7 D.8 組卷:173引用:1難度:0.6 -
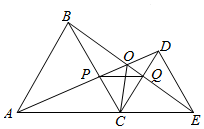 7.已知,如圖,C為線段AE上一動點(不與A,E重合),在AE同側分別作等邊三角形ABC和等邊三角形CDE,AD與BE交于點O,AD與BC交于點P,BE與CD交于點Q,連接PQ,OC,以下四個結論:①AD=BE;②△CPQ是等邊三角形;③AD⊥BC;④OC平分∠AOE.其中正確的結論是( )
7.已知,如圖,C為線段AE上一動點(不與A,E重合),在AE同側分別作等邊三角形ABC和等邊三角形CDE,AD與BE交于點O,AD與BC交于點P,BE與CD交于點Q,連接PQ,OC,以下四個結論:①AD=BE;②△CPQ是等邊三角形;③AD⊥BC;④OC平分∠AOE.其中正確的結論是( )A.①、② B.③、④ C.①、②、③ D.①、②、④ 組卷:1318引用:5難度:0.5
三、解答題。(共55分)
-
21.△ABC中,AB=AC,∠A=40°,D、E分別是AB,AC上的不動點.且BD+CE=BC,點P是BC上的一動點.
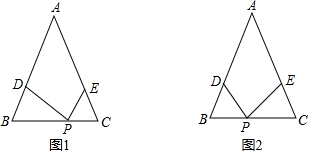
(1)當PC=CE時(如圖1),求∠DPE的度數;
(2)若PC=BD時(如圖2),求∠DPE的度數還會與(1)的結果相同嗎?若相同,請寫出求解過程;若不相同,請說明理由.組卷:892引用:2難度:0.5 -
 22.如圖,已知△ABC中,AB=AC=12cm,BC=10cm,點D為AB的中點.如果點P在線段BC上以2cm/s的速度由點B向C點運動,同時,點Q在線段AC上由點A向C點以4cm/s的速度運動.
22.如圖,已知△ABC中,AB=AC=12cm,BC=10cm,點D為AB的中點.如果點P在線段BC上以2cm/s的速度由點B向C點運動,同時,點Q在線段AC上由點A向C點以4cm/s的速度運動.
(1)若點P、Q兩點分別從B、A兩點同時出發,經過2秒后,△BPD與△CQP是否全等?請說明理由;
(2)若點P、Q兩點分別從B、A兩點同時出發,△CPQ的周長為16cm,設運動時間為t,問:是否存在某一時刻t,使得△CPQ是等腰三角形?如存在,請求出t的值,若不存在,請說明理由.組卷:611引用:4難度:0.5


