2023-2024學年浙江省杭州十四中康橋校區高二（上）段考數學試卷（10月份）

一、單選題（本大題共8小題，共40.0分。在每小題列出的選項中，選出符合題目的一項）

• 1．在平面直角坐標系中，直線l：x+

  3

  y+1=0的傾斜角為（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：234引用：8難度：0.7

  解析

• 2．已知直線l的一個方向向量

  m

  =（2，-1，3），且直線l過A（0，y,3）和B（-1，2，z）兩點，則y-z=（　　）

  A．0

  B．1

  C． 3 2

  D．3
  組卷：428引用：8難度：0.9

  解析

• 3．我國著名數學家華羅庚曾說：“數缺形時少直觀，形缺數時難入微，數形結合百般好，隔裂分家萬事休．”在數學的學習和研究中，常用函數的圖象來研究函數的性質，也常用函數的解析式來研究函數圖象的特征．我們從這個商標中抽象出一個圖象如圖，其對應的函數可能是（　　）

  A． f （ x ） = 1 | x - 1 |

  B． f （ x ） = 1 | | x | - 1 |

  C． f （ x ） = 1 x 2 - 1

  D． f （ x ） = 1 x 2 + 1
  組卷：775引用：55難度：0.8

  解析

• 4．直線x+2ay-1=0與（a-1）x+ay+1=0平行，則a等于（　　）

  A． 3 2

  B． 3 2 或0

  C．0

  D．-2或0
  組卷：56引用：7難度：0.9

  解析

• 5．已知點A（

  3

  ，2），B（4，-3），若直線l過點P（0，1）與線段AB相交，則直線l的傾斜角的取值范圍是（　　）

  A． [ π 3 ， 5 π 6 ]	B．[ π 6 ， 2 π 3 ]
  C． [ 0 ， π 6 ] ∪ [ 3 π 4 ， π ）	D． [ 0 ， π 3 ] ∪ [ 5 π 6 ， π ）
  組卷：1105引用：5難度：0.8

  解析

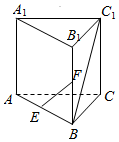• 6．如圖所示，在三棱柱ABC-A₁B₁C₁中，AA₁⊥底面ABC，AB=BC=AA₁，∠ABC=90°，點E、F分別是棱AB、BB₁的中點，則直線EF和BC₁所成的角是（　　）

  A．45°

  B．60°

  C．90°

  D．120°
  組卷：280引用：23難度：0.9

  解析

• 7．已知a＞0，b＞0，直線l₁：x+（a-4）y+1=0，l₂：2bx+y-2=0，且l₁⊥l₂，則

  a

  +

  2

  a

  +

  1

  +

  1

  2

  b

  的最小值為（　　）

  A．2

  B．4

  C． 4 5

  D． 9 5
  組卷：1056引用：8難度：0.6

  解析

四、解答題（本大題共6小題，共70.0分。解答應寫出文字說明，證明過程或演算步驟）

• 21．函數f（x）=Asin（ωx+φ）

  （

  A

  ＞

  0

  ，

  0

  ＜

  ω

  ＜

  16

  ，

  0

  ＜

  φ

  ＜

  π

  2

  ）

  在R上的最大值為

  2

  ，f（0）=1．
  （1）若點

  （

  π

  8

  ，

  2

  ）

  在f（x）的圖象上，求函數f（x）圖象的對稱中心；
  （2）將函數y=f（x）的圖象向右平移

  π

  4

  ω

  個單位，再將所得的圖象縱坐標不變，橫坐標縮小到原來的

  1

  2

  ，得函數y=g（x）的圖象，若y=g（x）在

  [

  0

  ，

  π

  8

  ]

  上為增函數，求ω的最大值．
  組卷：475引用：4難度：0.4

  解析

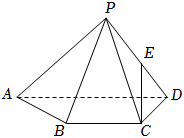• 22．如圖，四棱錐P-ABCD中，△PAD是以AD為斜邊的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB=2，E為PD的中點．
  （1）證明：CE∥平面PAB；
  （2）求直線CE與平面PAB間的距離．
  組卷：549引用：5難度：0.4

  解析