2021-2022學年黑龍江省鶴崗一中高一（下）開學數學試卷

一、單選題

• 1．命題“?x∈R，e^x-1≥x”的否定是（　　）

  A．?x∈R，ex-1≥x	B．?x∈R，ex-1≤x
  C．?x∈R，ex-1＜x	D．?x∈R，ex-1＜x
  組卷：32引用：2難度：0.9

  解析

• 2．函數f（x）=

  ln

  （

  x

  +

  1

  ）

  x

  -

  2

  的定義域是（　　）

  A．（-1，+∞）	B．（-1，2）∪（2，+∞）
  C．（-1，2）	D．[-1，2）∪（2，+∞）
  組卷：1409引用：7難度：0.8

  解析

• 3．已知α是第二象限角，且sinα=

  3

  5

  ，則tanα=（　　）

  A． - 3 4

  B． 3 4

  C． 4 3

  D． - 4 3
  組卷：187引用：9難度：0.7

  解析

• 4．函數f（x）=e^x+x-2的零點所在的區間是（　　）

  A．（-1，0）

  B．（0，1）

  C．（1，2）

  D．（2，3）
  組卷：189引用：6難度：0.9

  解析

• 5．設f（x）是定義域R，最小正周期為

  3

  π

  2

  的函數，若f（x）=

  cosx （ - π 2 ≤ x ＜ 0 ）

  sinx （ 0 ≤ x ≤ π ）

  ，則f（-

  15

  π

  4

  ）的值等于（　　）

  A．1

  B． 2 2

  C．0

  D． - 2 2
  組卷：122引用：9難度：0.9

  解析

• 6．若函數

  f

  （

  x

  ）

  =

  tan

  （

  ωx

  +

  π

  4

  ）

  （

  ω

  ＞

  0

  ）

  的最小正周期為π，則（　　）

  A．f（2）＞f（0）＞f（- π 5 ）	B．f（0）＞f（2）＞f（- π 5 ）
  C．f（0）＞f（- π 5 ）＞f（2）	D．f（- π 5 ）＞f（0）＞f（2）
  組卷：315引用：3難度：0.8

  解析

• 7．已知函數

  f

  （

  x

  ）

  =

  x 2 - 2 ax , x ≥ 1

  ax - 1 ， x ＜ 1

  是R上的增函數，則實數a的取值范圍是（　　）

  A．（0， 2 3 ）

  B．（0， 2 3 ]

  C．（0，1）

  D．（0，1]
  組卷：281引用：9難度：0.7

  解析

四、解答題

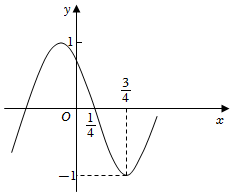• 21．函數f（x）=cos（ωx+φ）（ω＞0，0＜φ＜π）的部分圖象如圖所示．
  （1）求函數f（x）的單調遞減區間；
  （2）將f（x）的圖象向右平移

  1

  2

  個長度單位，再將所得圖象上所有點的橫坐標伸長為原來的π倍（縱坐標不變），得到函數g（x）的圖象，若g（x）=a-1在x∈[0，

  7

  π

  4

  ]上有兩個解，求a的取值范圍．
  組卷：314引用：3難度：0.5

  解析

• 22．某公司生產一種兒童玩具，每年的玩具起步生產量為1萬件；經過市場調研，生產該玩具需投入年固定成本2萬元，每生產x萬件，需另投入流動成本W（x）萬元，在年產量不足6萬件時，

  W

  （

  x

  ）

  =

  1

  2

  （

  log

  2

  x

  ）

  2

  -

  2

  lo

  g

  2

  x

  -

  10

  +

  8

  x

  ；在年產量不小于6萬件時，

  W

  （

  x

  ）

  =

  9

  x

  +

  81

  x

  -

  42

  ．每件玩具售價8元．通過市場分析．該公司生產的玩具能當年全部售完．
  （1）寫出年利潤P（x）（萬元）關于年產量x（萬件）的函數解析式；
  （注：年利潤=年銷售收入-固定成本-流動成本）
  （2）年產量為多少萬件時，該公司這款玩具的生產中所獲利潤最大？最大利潤是多少？
  組卷：9引用：3難度：0.5

  解析