2023-2024學年福建省廈門一中高三（上）第一次月考數學試卷（10月份）
發布：2024/9/1 0:0:9
一、選擇題：本題8小題，每題5分，共40分.在每題給出的四個選項中只有一項是符合題目要求的.
-
1．已知集合A={0，1，2，3}，B={x|x=n2-1，n∈A}，P=A∪B，則P的子集共有（ ）
組卷：735引用：8難度：0.7 -
2．若（1+i）z=2i,其中i為虛數單位，則
=（ ）zz組卷：54引用：2難度：0.8 -
3．已知函數f（x）的定義域為[1，+∞），數列{an}滿足an=f（n），則“數列{an}為遞增數列”是“函數f（x）為增函數”的（ ）
組卷：134引用：5難度：0.8 -
4．如圖所示，九連環是中國傳統民間智力玩具，以金屬絲制成9個圓環，解開九連環共需要256步，解下或套上一個環算一步，且九連環的解下和套上是一對逆過程．九連環把玩時按照一定得程序反復操作，可以將九個環全部從框架上解下或者全部套上．將第n個圓環解下最少需要移動的次數記為an（n≤9，n∈N*），已知a1=1，a2=1，按規則有an=an-1+2an-2+1（n≥3，n∈N*），則解下第5個圓環最少需要移動的次數為（ ）組卷：78引用：1難度：0.5 -
5．用一個平行于圓錐C底面的平面截該圓錐得到一個圓臺，若圓臺上底面和下底面半徑之比為
，則該圓臺與圓錐C的體積之比為（ ）23組卷：75引用：2難度：0.7 -
6．已知角α的終邊落在直線y=-2x上，則2cos2α+sin2α+3sin2α的值為（ ）
組卷：76引用：2難度：0.7 -
7．已知雙曲線
的左、右焦點分別為F1、F2，過F2作一條直線與雙曲線右支交于A、B兩點，坐標原點為O，若|OA|=x2a2-y2b2=1（a＞0，b＞0），|BF1|=5a,則該雙曲線的離心率為（ ）a2+b2組卷：188引用：2難度：0.5
四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.
-
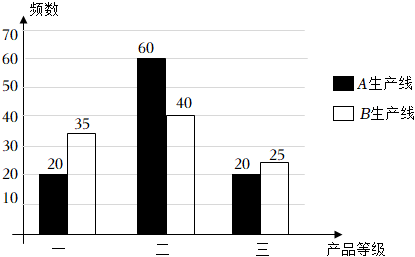21．某工廠A，B兩條相互獨立的生產線生產同款產品，在產量一樣的情況下通過日常監控得知，A，B生產線生產的產品為合格品的概率分別為p和2p-1（0.5≤p≤1）．
（1）從A，B生產線上各抽檢一件產品，若使得至少有一件合格的概率不低于99.5%，求p的最小值p0．
（2）假設不合格的產品均可進行返工修復為合格品，以（1）中確定的p0作為p的值．
①已知A，B生產線的不合格品返工后每件產品可分別挽回損失5元和3元，若從兩條生產線上各隨機抽檢1000件產品，以挽回損失的平均數為判斷依據，估計哪條生產線的挽回損失較多？
②若最終的合格品（包括返工修復后的合格品）按照一、二、三等級分類后，每件可分別獲利10元、8元、6元，現從A，B生產線的最終合格品中各隨機抽取100件進行檢測，結果統計如圖：用樣本的頻率分布估計總體分布，記該工廠生產一件產品的利潤為X，求X的分布列并估計該廠產量2000件時利潤的期望值．組卷：207引用：9難度：0.8 -
22．函數f（x）=sinx-ax+1．
（1），求f（x）的單調區間；a=12
（2）若f（x）≥cosx在x∈[0，π]上恒成立，求實數a的取值范圍；
（3）令函數g（x）=f（x）+ax-1，求證：．g（π15）+g（2π15）+g（3π15）+…+g（8π15）≥225組卷：320引用：3難度：0.1