人教新版九年級上學期《第24章 圓》2020年中考真題套卷（1）

一、選擇題（共10小題）

• 1．在△ABC中，若O為BC邊的中點，則必有：AB²+AC²=2AO²+2BO²成立．依據以上結論，解決如下問題：如圖，在矩形DEFG中，已知DE=4，EF=3，點P在以DE為直徑的半圓上運動，則PF²+PG²的最小值為（　　）

  A． 10

  B． 19 2

  C．34

  D．10
  組卷：4089引用：24難度：0.9

  解析

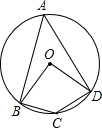• 2．如圖，四邊形ABCD為⊙O的內接四邊形，已知∠BCD為120°，則∠BOD的度數為（　　）

  A．100°

  B．110°

  C．120°

  D．130°
  組卷：3605引用：30難度：0.8

  解析

• 3．以坐標原點O為圓心，作半徑為2的圓，若直線y=-x+b與⊙O相交，則b的取值范圍是（　　）

  A．0≤b＜2 2

  B．-2 2 ≤ b ≤ 2 2

  C．-2 3 ＜ b ＜ 2 3

  D．-2 2 ＜b＜2 2
  組卷：6313引用：31難度：0.7

  解析

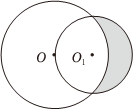• 4．如圖，一個半徑為1的⊙O₁經過一個半徑為

  2

  的⊙O的圓心，則圖中陰影部分的面積為（　　）

  A．1

  B． 1 2

  C． 2

  D． 2 2
  組卷：660引用：4難度：0.7

  解析

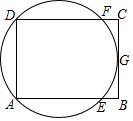• 5．如圖，矩形ABCD中，G是BC的中點，過A、D、G三點的圓O與邊AB、CD分別交于點E、點F，給出下列說法：（1）AC與BD的交點是圓O的圓心；（2）AF與DE的交點是圓O的圓心；（3）BC與圓O相切，其中正確說法的個數是（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：2703引用：20難度：0.7

  解析

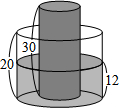• 6．如圖，有一內部裝有水的直圓柱形水桶，桶高20公分；另有一直圓柱形的實心鐵柱，柱高30公分，直立放置于水桶底面上，水桶內的水面高度為12公分，且水桶與鐵柱的底面半徑比為2：1．今小賢將鐵柱移至水桶外部，過程中水桶內的水量未改變，若不計水桶厚度，則水桶內的水面高度變為多少公分？（　　）

  A．4.5

  B．6

  C．8

  D．9
  組卷：754引用：5難度：0.7

  解析

• 7．對下列生活現象的解釋其數學原理運用錯誤的是（　　）

  A．把一條彎曲的道路改成直道可以縮短路程是運用了“兩點之間線段最短”的原理

  B．木匠師傅在刨平的木板上任選兩個點就能畫出一條筆直的墨線是運用了“直線外一點與直線上各點連接的所有線段中，垂線段最短”的原理

  C．將自行車的車架設計為三角形形狀是運用了“三角形的穩定性”的原理

  D．將車輪設計為圓形是運用了“圓的旋轉對稱性”的原理
  組卷：2683引用：11難度：0.7

  解析

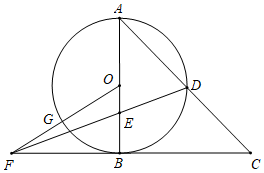• 8．如圖，在△ABC中，AB=BC，∠ABC=90°，以AB為直徑的⊙O交AC于點D，點E為線段OB上的一點，OE：EB=1：

  3

  ，連接DE并延長交CB的延長線于點F，連接OF交⊙O于點G，若BF=2

  3

  ，則

  ?

  BG

  的長是（　　）

  A． π 3

  B． π 2

  C． 2 π 3

  D． 3 π 4
  組卷：1543引用：4難度：0.6

  解析

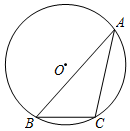• 9．如圖，⊙O是△ABC的外接圓，半徑為2cm,若BC=2cm,則∠A的度數為（　　）

  A．30°

  B．25°

  C．15°

  D．10°
  組卷：3787引用：29難度：0.5

  解析

• 10．在圓中，與半徑相等的弦所對的圓心角的度數為（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  組卷：1104引用：8難度：0.5

  解析

三、解答題（共10小題）

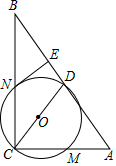• 29．如圖，在Rt△ABC中，∠ACB=90°，CD是斜邊AB上的中線，以CD為直徑的⊙O分別交AC、BC于點M、N，過點N作NE⊥AB，垂足為E．
  （1）若⊙O的半徑為

  5

  2

  ，AC=6，求BN的長；
  （2）求證：NE與⊙O相切．
  組卷：4124引用：23難度：0.6

  解析

• 30．如圖，在⊙O中，

  ?

  AB

  =2

  ?

  AC

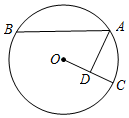  ，AD⊥OC于D．求證：AB=2AD．
  組卷：3396引用：17難度：0.6

  解析