當前位置：試卷中心 > 試卷詳情

2022-2023學年安徽省六安市裕安區新安中學（1-10班）高一（下）期中數學試卷

發布：2024/7/22 8:0:9

一、單選題：本題共8小題，每小題5分，共40分.在每個小題給出的四個選項中，只有一項是符合題目要求的.

1．sin（-120°）tan225°的值為（　　）
A．
-
3
2
B．
3
2
C．
1
2
D．
-
1
2
組卷：130引用：3難度：0.7
解析
2．已知向量
a
=（2，1），
b
=
（
x
,-
2
）
，若
a
∥
b
，則
a
-
2
b
=（　　）
A．（3，-1） B．（2，1） C．（-2，-1） D．（10，5）
組卷：41引用：2難度：0.7
解析
3．已知單位向量
a
、
b
滿足
a
⊥
b
，則
a
?
（
2
a
-
b
）
=（　　）
A．0 B．
1
2
C．1 D．2
組卷：24引用：2難度：0.7
解析
4．已知角θ終邊經過點（1，-2），則
sin
（
π
2
+
θ
）
+
2
sin
（
π
+
θ
）
cos
（
π
-
θ
）
+
sin
（
2
π
-
θ
）
的值為（　　）
A．-5 B．5 C．
-
5
3
D．
5
3
組卷：750引用：3難度：0.7
解析
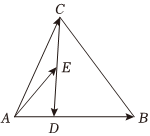5．如圖，在△ABC中，BD=2AD，E為CD的中點，設
AB
=
a
，
AC
=
b
，則
AE
=（　　）
A．
1
3
a
+
1
2
b
B．
1
4
a
+
1
2
b
C．
1
5
a
+
1
2
b
D．
1
6
a
+
1
2
b
組卷：269引用：5難度：0.7
解析
6．若平面向量
a
與
b
的夾角為60°，
a
=（2，0），
|
b
|
=
1
，則
|
2
a
+
b
|
等于（　　）
A．
3
B．
2
3
C．4 D．
21
組卷：59引用：2難度：0.8
解析
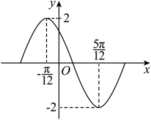7．函數f（x）=Asin（ωx+φ）（A＞0，ω＞0且|φ|＜π）在一個周期內的圖象如圖所示，下列結論正確的是（　　）
A．
f
（
x
）
=
2
sin
（
2
x
+
π
3
）
B．f（x）在
[
-
π
，-
π
2
]
上單調遞減
C．
f
（
5
π
6
）
=
3
D．把y=2sin2x的圖象向左平移
2
π
3
個單位可以得到f（x）的圖象
組卷：136引用：2難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，第17小題10分，其余小題每題12分，共70分.解答題應寫出文字說明、證明過程或演算步驟.

21．已知點O是△ABC外接圓的圓心，點M是BC邊的中點．
（1）若AM=4，BC=6，求
AB
?
AC
的值；
（2）若AB=7，
AC
=
23
，求
AO
?
AM
的值．
組卷：28引用：2難度：0.4
解析
22．已知O為坐標原點，對于函數f（x）=asinx+bcosx,稱向量
OM
=
（
a
,
b
）
為函數f（x）的伴隨向量，同時稱函數f（x）為向量
OM
的伴隨函數．
（1）設函數
g
（
x
）
=
sin
（
x
+
5
π
6
）
+
cos
（
3
π
2
+
x
）
，試求g（x）的伴隨向量的坐標；
（2）記向量
ON
=
（
1
，
3
）
的伴隨函數為f（x），當
f
（
x
）
=
8
5
且
x
∈
（
-
π
3
，
π
6
）
時，求sinx的值；
（3）設向量
OP
=
（
2
λ
，-
2
λ
）
，λ∈R的伴隨函數為u（x），
OQ
=
（
1
，
1
）
的伴隨函數為v（x），記函數h（x）=u（x）+v²（x），求h（x）在[0，π]上的最大值．
組卷：62引用：6難度：0.5
解析