當(dāng)前位置：試卷中心 > 試卷詳情

2021-2022學(xué)年河北省秦皇島市盧龍第二高級(jí)中學(xué)高二（上）期中數(shù)學(xué)試卷

發(fā)布：2024/11/24 4:30:2

1．已知直線a的傾斜角為45°，則a的斜率是（　　）
A．1 B．2 C．3 D．4
組卷：191引用：5難度：0.9
解析
2．圓心在（-1，0），半徑為
5
的圓的方程為（　　）
A．（x+1）²+y²=5 B．（x+1）²+y²=25
C．
（
x
+
1
）
2
+
y
2
=
5
D．（x-1）²+y²=25
組卷：514引用：4難度：0.8
解析
3．下列直線中，與直線x-2y+1=0垂直的是（　　）
A．2x-y-3=0 B．x-2y+3=0 C．2x+y+5=0 D．x+2y-5=0
組卷：384引用：8難度：0.9
解析
4．已知直線3x+2y-3=0和6x+my+1=0互相平行，則它們之間的距離是（　　）
A．4 B．
2
13
13
C．
5
13
26
D．
7
13
26
組卷：636引用：28難度：0.9
解析
5．若圓心坐標(biāo)為（2，-1）的圓被直線x-y-1=0截得的弦長(zhǎng)為
2
2
，則這個(gè)圓的方程是（　　）
A．（x-2）²+（y+1）²=2 B．（x-2）²+（y+1）²=4
C．（x-2）²+（y+1）²=8 D．（x-2）²+（y+1）²=6
組卷：83引用：3難度：0.7
解析
6．若三棱錐P-ABC的三條側(cè)棱兩兩垂直，且滿足PA=PB=PC=1，則點(diǎn)P到平面ABC的距離是（　　）
A．
6
6
B．
6
3
C．
3
6
D．
3
3
組卷：105引用：11難度：0.5
解析
7．已知直三棱柱ABC-A₁B₁C₁中，∠ABC=60°，AB=2，BC=CC₁=1，則異面直線AB₁與BC₁所成角為（　　）
A．
π
2
B．
π
3
C．
π
4
D．
π
6
組卷：76引用：5難度：0.8
解析

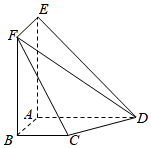21．如圖所示，AE⊥平面ABCD，四邊形AEFB為矩形，BC∥AD，BA⊥AD，AE=AD=2AB=2BC=2．
（1）求證：CF∥平面ADE；
（2）求平面CDF與平面AEFB所成銳二面角的余弦值．
組卷：10引用：1難度：0.7
解析
22．在①平面PAB⊥平面ABCD，②AP⊥CD，③BC⊥平面PAB這三個(gè)條件中任選一個(gè)，補(bǔ)充在下面的問題中并作答．如圖，在四棱錐P-ABCD中，底面ABCD是梯形，點(diǎn)E在BC上，AD∥BC，AB⊥AD，AB⊥AP，BC=2AB=2AD=2AP=4BE=4，且_____．
（1）求證：平面PDE⊥平面PAC；
（2）求直線PE與平面PAC所成角的正弦值．
組卷：96引用：3難度：0.5
解析