2018-2019學年云南省玉溪市峨山一中高二（上）期中數學試卷（文科）

一、選擇題：本題共12小題，每小題5分，共60分.

• 1．已知集合A={x|-1＜x＜2}，B={x|0＜x＜3}，則A∪B=（　　）

  A．（-1，3）

  B．（-1，0）

  C．（0，2）

  D．（2，3）
  組卷：4707引用：83難度：0.9

  解析

• 2．不等式x²+2x-3≥0的解集為（　　）

  A．{x|x≤-1或x≥3}

  B．{x|-1≤x≤3}

  C．{x|x≤-3或x≥1}

  D．{x|-3≤x≤1}
  組卷：79引用：9難度：0.9

  解析

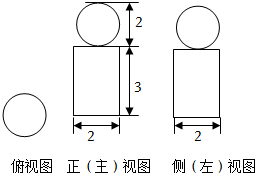• 3．如圖是一個幾何體的三視圖，根據圖中數據，可得該幾何體的體積是
  （　　）

  A． 10 π 3

  B． 13 π 3

  C． 11 π 3

  D． 8 π 3
  組卷：19引用：5難度：0.9

  解析

• 4．函數f（x）=

  x

  +

  2

  +ln（1-x）的定義域為（　　）

  A．[-2，1）

  B．（-2，1]

  C．[-2，1]

  D．（1，+∞）
  組卷：97引用：4難度：0.8

  解析

• 5．如果x,y滿足約束條件

  x - y + 1 ≥ 0

  x + y - 2 ≤ 0

  x - 2 y ≤ 0

  ，則z=2x+y的最大值是（　　）

  A．-5

  B． 5 2

  C． 10 3

  D．5
  組卷：8引用：3難度：0.7

  解析

• 6．已知sin

  α

  =

  2

  5

  ，則cos2α=（　　）

  A． 7 25

  B． - 7 25

  C． 17 25

  D． - 17 25
  組卷：173引用：6難度：0.9

  解析

• 7．函數y=

  1

  2

  lnx+x-2的零點所在的區間是（　　）

  A．（ 1 e ，1）

  B．（1，2）

  C．（e,3）

  D．（2，e）
  組卷：257引用：20難度：0.8

  解析

三、解答題：共70分.解答應寫出文字說明、證明過程或演算步驟.

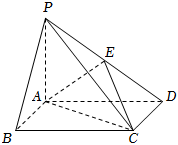• 21．如圖，四棱錐P-ABCD中，底面ABCD為矩形，PA⊥面ABCD，E為PD的中點．
  （1）證明：PB∥平面AEC；
  （2）設AP=1，AD=

  3

  ，AB=

  3

  2

  ，求A到平面PBC的距離．
  組卷：70引用：2難度：0.5

  解析

• 22．已知{a_n}是公差為3的等差數列，數列{b_n}滿足b₁=1，b₂=

  1

  3

  ，a_nb_n+1+b_n+1=nb_n．
  （Ⅰ）求{a_n}的通項公式；
  （Ⅱ）求{b_n}的前n項和．
  組卷：10533引用：41難度：0.5

  解析