2021-2022學年北京八中高二（下）期末數學試卷

一、選擇題共12小題，每小題5分，共60分。在每小題列出的四個選項中，選出符合題目要求的一項。

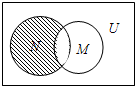• 1．設全集U是實數集R，M={x||x|≥2}，N={x|1＜x＜3}，則圖中陰影部分所表示的集合是（　　）

  A．{x|-2＜x＜1}

  B．{x|-2＜x＜2}

  C．{x|1＜x＜2}

  D．{x|x＜2}
  組卷：195引用：11難度：0.9

  解析

• 2．設a,b,c為非零實數，且a＞b＞c,則下列判斷中正確的是（　　）

  A．a+b＞c

  B．ab＞c2

  C．ac2＞bc2

  D． 1 a + 1 b ＜ 2 c
  組卷：108引用：1難度：0.7

  解析

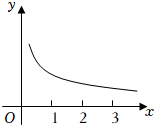• 3．已知函數f（x）的圖象如圖所示，那么下列各式正確的是（　　）

  A．f′（1）＜f′（2）＜f′（3）＜0	B．f′（1）＞f′（2）＞f′（3）＞0
  C．f′（3）＜f′（2）＜f′（1）＜0	D．f′（3）＞f′（2）＞f′（1）＞0
  組卷：181引用：3難度：0.7

  解析

• 4．一個關于自然數n的命題，已經驗證知n=1時命題成立，并在假設n=k（k為正整數）時命題成立的基礎上，證明了當n=k+2時命題成立，那么綜上可知，該命題對于（　　）

  A．一切自然數成立	B．一切正整數成立
  C．一切正奇數成立	D．一切正偶數成立
  組卷：116引用：5難度：0.8

  解析

• 5．甲、乙兩人獨立地解同一問題，甲解出這個問題的概率

  1

  4

  ，乙解出這個問題的概率是

  1

  2

  ，那么其中至少有1人解出這個問題的概率是（　　）

  A． 3 4

  B． 1 8

  C． 7 8

  D． 5 8
  組卷：177引用：6難度：0.8

  解析

• 6．已知二次函數f（x）=ax²+2x+c（x∈R）的值域為[0，+∞），則

  1

  c

  +

  4

  a

  的最小值為（　　）

  A．4

  B．6

  C．8

  D．10
  組卷：337引用：3難度：0.7

  解析

• 7．下列函數中，在（0，+∞）為增函數的是（　　）

  A．y=tanx

  B．y= 1 x

  C．y=e|x-1|

  D．y=x+ 1 x + 1
  組卷：374引用：2難度：0.8

  解析

三、解答題共5小題，共65分。解答應寫出文字說明，演算步驟或證明過程。

• 21．已知函數f（x）=e^x+x²+ax（a∈R），其中e是自然對數的底數．
  （Ⅰ）若f（x）在x=1處取得極小值，求a的值；
  （Ⅱ）若存在x₁，x₂（x₁≠x₂），使得f（x₁）=f（x₂），且x₁+x₂=2，求a的取值范圍．
  組卷：136引用：1難度：0.5

  解析

• 22．設A為非空集合，令A×A={（x,y）|x,y∈A}，則A×A的任意子集R都叫做從A到A的一個關系（Relation），簡稱A上的關系．
  例如A={0，1，2}時，R₁={（0，2）}，R₂=A×A，R₃=?，R₄={（0，0），（2，1）}等都是A上的關系．
  設R為非空集合A上的關系．給出如下定義：
  ①（自反性）若?x∈A，有（x,x）∈R，則稱R在A上是自反的；
  ②（對稱性）若?（x,y）∈R，有（y,x）∈R，則稱R在A．上是對稱的；
  ③（傳遞性）若?（x,y），（y,z）∈R，有（x,z）∈R，則稱R在A．上是傳遞的；
  如果R同時滿足這3條性質，則稱R為A上的等價關系．
  （Ⅰ）已知A={0，1，2}，按要求填空：
  （ⅰ）用列舉法寫出A×A=

  ；
  （ⅱ）A上的關系有

  個（用數值作答）；
  （ⅲ）用列舉法寫出A上的所有等價關系：{（0，0），（1，1），（2，2）}，{（0，0），（1，1），（2，2），（0，1），（1，0）}，{（0，0），（1，1），（2，2），（0，2），（2，0）}，
  

  ，

  共5個．
  （Ⅱ）設R₁，和R₂是某個非空集合A上的關系，證明：
  （ⅰ）若R₁，R₂是自反的和對稱的，則R₁∪R₂也是自反的和對稱的：
  （ⅱ）若R₁，R₁是傳遞的，則R₁∩R₂也是傳遞的．
  （Ⅲ）若給定的集合A有n個元素（n≥4）A₁，A₂，?A_m（2≤m≤n）為A的非空子集，滿足A₁∪A₂∪?∪A_m=A且兩兩交集為空集．
  求證：R=（A₁×A₁）∪（A₂×A₂）∪?∪（A_m×A_m）為A上的等價關系．
  組卷：282引用：1難度：0.3

  解析