2023-2024學年安徽省合肥一中高三（上）第一次質檢數學試卷（10月份）

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知函數

  f

  （

  x

  ）

  =

  2

  x

  +

  3

  +

  lo

  g

  2

  （

  2

  -

  x

  ）

  ，則f（x）的定義域為（　　）

  A．（-3，2）

  B．[-3，2）

  C．（-3，2]

  D．[-3，2]
  組卷：197引用：4難度：0.9

  解析

• 2．已知等比數列{a_n}滿足a₁+a₃=10，a₄+a₆=80，則數列{a_n}前8項的和為（　　）

  A．254

  B．256

  C．510

  D．512
  組卷：297引用：2難度：0.8

  解析

• 3．將

  y

  =

  sin

  （

  x

  -

  π

  4

  ）

  圖象上每一個點的橫坐標變為原來的3倍（縱坐標不變），得到y=g（x）的圖象，再將y=g（x）的圖象向左平移

  π

  6

  個單位長度，得到y=φ（x）的圖象，則y=φ（x）的解析式為（　　）

  A． y = sin （ 3 x - π 12 ）	B． y = sin （ 3 x + π 4 ）
  C． y = sin （ 1 3 x - π 12 ）	D． y = sin （ 1 3 x - 7 π 36 ）
  組卷：68引用：2難度：0.5

  解析

• 4．已知函數

  f

  （

  x

  ）

  =

  （

  1

  3

  ）

  2

  x

  2

  -

  ax

  在區間（2，+∞）上單調遞減，則a的取值范圍是（　　）

  A．（-∞，8]

  B．（-∞，8）

  C．[8，+∞）

  D．（8，+∞）
  組卷：192引用：11難度：0.7

  解析

• 5．已知函數f（x）=x（x-3）（x-3²）（x-3³）（x-3⁴）（x-3⁵），則f'（0）=（　　）

  A．315

  B．314

  C．-314

  D．-315
  組卷：230引用：1難度：0.8

  解析

• 6．函數f（x）=x³+sin3x的圖象大致為（　　）

  A．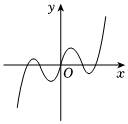

  B．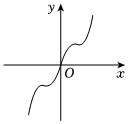

  C．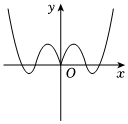

  D．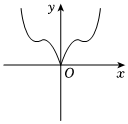
  組卷：16引用：1難度：0.7

  解析

• 7．數學家斐波那契在研究兔子繁殖問題時，發現有這樣一個數列{a_n}：1，1，2，3，5，8…，其中從第3項起，每一項都等于它前面兩項之和，即a₁=a₂=1，a_n+2=a_n+1+a_n，這樣的數列稱為“斐波那契數列”．若a_m=2（a₃+a₆+a₉+…+a₁₇₄）+1，則m=（　　）

  A．175

  B．176

  C．177

  D．178
  組卷：207引用：6難度：0.5

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知函數f（x）=x²+lnx.
  （1）求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）證明：f（x）＜e^x+x²-2．
  組卷：39引用：1難度：0.5

  解析

• 22．已知函數f（x）=a（e^x-x）-e^-x-x（a∈R）．
  （1）若a=e,求函數f（x）的單調區間；
  （2）當0＜a＜1時，x₁，x₂分別為函數f（x）的極大值點和極小值點，且f（x₁）+tf（x₂）＞0，求t的取值范圍．
  組卷：87引用：3難度：0.5

  解析