2022-2023學年山西大學附中高二（下）月考數學試卷（3月份）

一、單選題（每小題5分，共40分）

• 1．用數學歸納法證明 1+

  1

  2

  +

  1

  3

  +…+

  1

  2

  n

  -

  1

  ＜n（n∈N^*，n＞1）時，第一步應驗證不等式（　　）

  A． 1 + 1 2 ＜ 2	B． 1 + 1 2 + 1 3 ＜ 2
  C． 1 + 1 2 + 1 3 ＜ 3	D． 1 + 1 2 + 1 3 + 1 4 ＜ 3
  組卷：1410引用：58難度：0.9

  解析

• 2．數列1，3⁷，3¹⁴，3²¹，…中，3⁹⁸是這個數列的（　　）

  A．不在此數列中	B．第13項
  C．第14項	D．第15項
  組卷：267引用：10難度：0.9

  解析

• 3．等比數列{a_n}中，若a₁+a₂+a₃+a₄=3（a₁+a₃），則公比為（　　）

  A．1

  B．-2

  C．2

  D．2或-2
  組卷：281引用：6難度：0.8

  解析

• 4．在各項均不為零的等差數列{a_n}中，若a_n+1-

  a

  2

  n

  +a_n-1=0（n≥2），則S_2n-1-4n=（　　）

  A．-2

  B．0

  C．1

  D．2
  組卷：755引用：33難度：0.9

  解析

• 5．一個首項為23，公差為整數的等差數列，如果前六項均為正數，第七項起為負數，則它的公差是（　　）

  A．-2

  B．-3

  C．-4

  D．-5
  組卷：722引用：18難度：0.9

  解析

• 6．1-7+7²-7³+?+（-7）²ⁿ=（　　）

  A． 1 - （ - 7 ） 2 n + 1 8	B． 1 - 7 2 n - 1 8
  C． 1 - （ - 7 ） 2 n - 1 8	D． 1 + 7 2 n + 2 8
  組卷：139引用：5難度：0.8

  解析

• 7．如圖第1個圖案的總點數記為a₁，第2個圖案的總點數記為a₂，第3個圖案的總點數記為a₃，…依此類推，第n個圖案的總點數記為a_n，則

  9

  a

  2

  a

  3

  +

  9

  a

  3

  a

  4

  +

  9

  a

  4

  a

  5

  +

  ?

  +

  9

  a

  2022

  a

  2023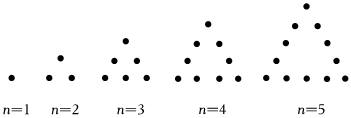

  =（　　）

  A． 2021 2022

  B． 2022 2021

  C． 2023 2022

  D． 2022 2023
  組卷：123引用：2難度：0.5

  解析

四、解答題（17題10分，其余每題12分.解答應寫出文字說明，證明過程或演算步驟.）

• 21．某地出現了蟲軎，農業科學家引入了“蟲害指數”數列{I_n}，{I_n}表示第n周的蟲害的嚴重程度，蟲害指數越大，嚴重程度越高．為了治理害蟲，需要環境整治、殺滅害蟲，然而由于人力資源有限，每周只能采取以下兩個策略之一：
  策略A：環境整治，“蟲害指數”數列滿足：I_n+1=1.02I_n-0.2．
  策略B：殺滅害蟲，“蟲害指數”數列滿足：I_n+1=1.08I_n-0.46．
  當某周“蟲害指數”小于1時，危機就在這周解除．
  （1）設第一周的蟲害指數I₁∈[0，8]，用哪一個策略將使第二周的蟲害的嚴重程度更小？
  （2）設第一周的蟲害指數I₁=3，如果每周都采用最優策略，蟲害的危機最快將在第幾周解除？
  組卷：50引用：4難度：0.5

  解析

• 22．已知等比數列{a_n}是遞減數列，{a_n}的前n項和為S_n，且

  1

  a

  1

  ，2S₂，8a₃成等差數列，3a₂=a₁+2a₃.數列{b_n}的前n項和為T_n，滿足T_n=n²+n,n∈N*．
  （Ⅰ）求{a_n}和{b_n}的通項公式；
  （Ⅱ）若c_n=

  a n b n ， n 是奇數 ，

  （ 3 n + 8 ） a n b n b n + 2 ， n 是偶數 ，

  求

  2

  n

  ∑

  i

  =

  1

  c

  i

  ．
  組卷：1027引用：8難度：0.4

  解析