2023-2024學年江西省南昌一中高二（上）第一次月考數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．若直線l的傾斜角為α，且45°≤α≤135°，則直線l斜率的取值范圍為（　　）

  A．[1，+∞）	B．（-∞，-1]
  C．[-1，1]	D．[1，+∞）∪（-∞，-1]
  組卷：108引用：2難度：0.8

  解析

• 2．已知直線l的一個方向向量為（2，-1），且經過點A（1，0），則直線l的方程為（　　）

  A．x-y-1=0

  B．x+y-1=0

  C．x-2y-1=0

  D．x+2y-1=0
  組卷：638引用：6難度：0.7

  解析

• 3．已知直線l₁：（3+2λ）x+（4+λ）y+（-2+2λ）=0（λ∈R），l₂：x+y-2=0，若l₁∥l₂，則l₁與l₂間的距離為（　　）

  A． 2 2

  B． 2

  C．2

  D．2 2
  組卷：525引用：3難度：0.7

  解析

• 4．若直線kx-y+2k-1=0恒過點A，點A也在直線mx+ny+2=0上，其中m,n均為正數，則mn的最大值為（　　）

  A． 1 4

  B． 1 2

  C．1

  D．2
  組卷：256引用：4難度：0.7

  解析

• 5．已知實數x,y滿足3x-4y-6=0，則

  x

  2

  +

  y

  2

  -

  2

  y

  +

  1

  的最小值為（　　）

  A．2

  B． 3 5

  C． 2 5

  D． 9 5
  組卷：52引用：3難度：0.8

  解析

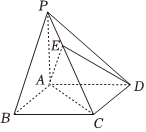• 6．我國古代數學名著《九章算術》中，將底面為矩形且一側棱垂直于底面的四棱錐稱為陽馬．如圖，四棱錐P-ABCD為陽馬，PA⊥平面ABCD，且EC=2PE，若

  DE

  =

  x

  AB

  +

  y

  AC

  +

  z

  AP

  ，則x+y+z=（　　）

  A．1

  B．2

  C． 1 3

  D． 5 3
  組卷：1318引用：34難度：0.7

  解析

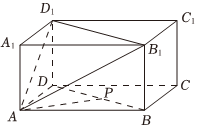• 7．如圖，在長方體ABCD-A₁B₁C₁D₁中，AA₁=AD=2，AB=3，P為線段BD上的動點，當直線AP與平面AB₁D₁所成角的正弦值取最大值時，

  DP

  DB

  =（　　）

  A． 1 2

  B． 1 3

  C． 2 5

  D． 4 13
  組卷：32引用：3難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步聚．

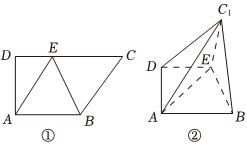• 21．圖①是直角梯形ABCD，AB∥CD，∠D=90°，四邊形ABCE是邊長為2的菱形，并且∠BCE=60°，以BE為折痕將△BCE折起，使點C到達C₁的位置，且AC₁=

  6

  ．
  （1）求證：平面BC₁E⊥平面ABED；
  （2）在棱DC₁上是否存在點P，使得點P到平面ABC₁的距離為

  15

  5

  ？若存在，求出直線EP與平面ABC₁所成角的正弦值；若不存在，請說明理由．
  組卷：511引用：18難度：0.6

  解析

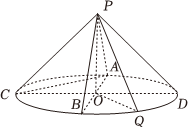• 22．如圖，圓錐的頂點為P，底面圓心為O，AB，CD為兩條互相垂直的直徑，Q是底面圓周上的動點（異于A，B），且C，Q在直徑AB的兩側．已知PO=OB=1．
  （1）若

  ∠

  QOB

  =

  π

  4

  ，求證：PQ⊥AC；
  （2）若在線段PQ上存在點T（異于P，Q），使得BT∥平面PAC，求∠QOB的取值范圍．
  組卷：33引用：2難度：0.5

  解析