2023年云南省昆明市中考數學診斷試卷（3月份）

一、選擇題（本大題共12小題，每小題只有一個正確選項，每小題3分，共36分）

• 1．徐志摩的《泰山日出》一文描寫了“泰山佛光”壯麗景象，3月份的泰山，山腳平均氣溫為零上9℃，記作+9℃，山頂平均氣溫為零下1℃，記作（　　）

  A．-1℃

  B．+1℃

  C．-9℃

  D．+9℃
  組卷：244引用：7難度：0.8

  解析

• 2．2023年2月25日，曲靖羅平花海馬拉松鳴槍開跑，約有11000名海內外專業運動員和馬拉松愛好者齊聚羅平，在奔跑中暢游最美花海賽道，共赴春日之約，數據11000用科學記數法可表示為（　　）

  A．0.11×105

  B．1.1×104

  C．11×103

  D．110×102
  組卷：26引用：3難度：0.7

  解析

• 3．在如圖所示的幾何體中，三視圖都是正方形的是（　　）

  A．

  B．

  C．

  D．
  組卷：24引用：1難度：0.8

  解析

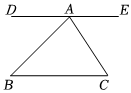• 4．如圖，直線DE經過點A，DE∥BC，∠BAC=90°，∠CAE=50°，則∠B的度數為（　　）

  A．60°

  B．50°

  C．40°

  D．30°
  組卷：66引用：1難度：0.6

  解析

• 5．下列運算正確的是（　　）

  A． 3 - 8 =2	B．|-2023|=2023
  C．2a6÷2a3=a2	D．（-ab3）2=-a2b6
  組卷：43引用：1難度：0.8

  解析

• 6．若

  x

  +

  2

  x

  有意義，則實數x的取值范圍為（　　）

  A．x＞-2

  B．x≥-2

  C．x＞-2且x≠0

  D．x≥-2且x≠0
  組卷：568引用：2難度：0.9

  解析

• 7．若正多邊形的一個外角是60°，則這個正多邊形的邊數是（　　）

  A．4

  B．5

  C．6

  D．7
  組卷：2338引用：23難度：0.8

  解析

• 8．按一定規律排列的單項式：2a,4a²，8a³，16a⁴，32a⁵，…，第n個單項式是（　　）

  A．2nan

  B．2nan

  C．2nan+1

  D．2nan+1
  組卷：85引用：1難度：0.6

  解析

三、解答題（本大題共8小題，共56分）

• 23．綜合與實踐
  【問題情境】
  數學活動課上，楊老師出示了教材上的一個問題：
  如圖1，四邊形ABCD是正方形，G是BC上的任意一點，DE⊥AG于點E，BF∥DE，交AG于點F，求證：AF-BF=EF．
  數學興趣小組的小明同學做出了回答，解題思路如下：
  由正方形的性質得到AB=AD，∠BAD=90°，
  再由垂直和平行可知∠AED=∠AFB=90°，
  再利用同角的余角相等得到∠ADE=∠BAF，
  則可根據“AAS”判定△ADE≌△BAF，
  得到AE=BF，所以AF-BF=AF-AE=EF．
  【建立模型】
  該數學小組小芳同學受此問題啟發，對上面的問題進行了改編，并提出了如下問題：
  （1）如圖2，四邊形ABCD是正方形，E，F是對角線AC上的點，BF∥DE，連接BE，DF．
  求證：四邊形BEDF是菱形；
  【模型拓展】
  該興趣小組的同學們在楊老師的指導下大膽嘗試，改變圖形模型，發現并提出新的探究點；
  （2）如圖3，若正方形ABCD的邊長為12，E是對角線AC上的一點，過點E作EG⊥DE，交邊BC于點G，連接DG，交對角線AC于點F，CF：EF=3：5，求FG?DF的值．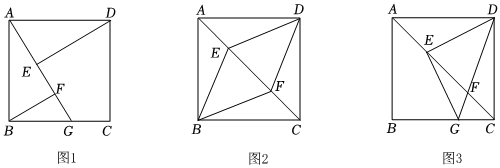
  
  組卷：676引用：1難度：0.4

  解析

• 24．已知二次函數解析式為y=x²-bx+2b-3．
  （1）當拋物線經過點（1，2）和點（m,n）時，等式m²-4m-n=-5是否成立？并說明理由；
  （2）已知點P（4，5）和點Q（-1，-5），且線段PQ與拋物線只有一個交點，求b的取值范圍．
  組卷：278引用：1難度：0.4

  解析