2021-2022學年廣東省廣州市華南師大附中高二（下）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的．

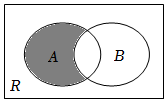• 1．已知集合A={x|1≤x≤5}，B={x|x²-3x-4≤0}，則如圖所示的陰影部分表示的集合為（　　）

  A．{x|4＜x≤5}

  B．{x|4≤x≤5}

  C．{x|1≤x≤4}

  D．{x|-1≤x≤1}
  組卷：130引用：4難度：0.8

  解析

• 2．已知△ABC中，角A，B，C所對的邊分別為a,b,c,且b=

  3

  a,A=

  π

  6

  ，則B等于（　　）

  A． π 6

  B． π 6 或 5 π 6

  C． π 3

  D． π 3 或 2 π 3
  組卷：69引用：1難度：0.7

  解析

• 3．某市一次高三模擬考試一共有3.2萬名考生參加，他們的總分ξ服從正態分布N（480，σ²），若P（430≤ξ≤530）=0.78，則總分高于530分的考生人數為（　　）

  A．2400

  B．3520

  C．8520

  D．12480
  組卷：312引用：7難度：0.8

  解析

• 4．已知向量

  a

  =

  （

  t

  ,

  1

  ）

  ，

  b

  =

  （

  t

  +

  2

  ，

  1

  ）

  ，若

  a

  ⊥

  b

  ，則實數t=（　　）

  A．-2

  B．-1

  C．1

  D．2
  組卷：229引用：4難度：0.9

  解析

• 5．西安中學抗疫志愿者小分隊中有3名男同學，2名女同學，現隨機選派2名同學前往社區參加志愿服務活動，在已知抽取的1名志愿者是女同學的情況下，2名都是女同學的概率是（　　）

  A． 1 4

  B． 1 5

  C． 1 7

  D． 1 10
  組卷：222引用：4難度：0.9

  解析

• 6．（

  x

  +

  1

  x

  ）（2x

  -

  1

  x

  ）⁵的展開式中常數項為（　　）

  A．-40

  B．-20

  C．20

  D．40
  組卷：162引用：7難度：0.7

  解析

• 7．九連環是我國從古至今廣泛流傳的一種益智游戲．它用九個圓環相連成串，以解開為勝．據明代楊慎《丹鉛總錄》記載“兩環互相貫為一得其關換，解之為三，又合而為一”．在某種玩法中，用a_n表示解下n（n≤9，n∈N^*）個圓環所需的移動最少次數，{a_n}滿足a₁=1，且a_n=

  2 a n - 1 - 1 ， n 為偶數

  2 a n - 1 + 2 ， n 為奇數

  ，則解下4個圓環所需的最少移動次數為（　　）

  A．7

  B．10

  C．12

  D．22
  組卷：198引用：10難度：0.8

  解析

四、解答題：共70分．解答應寫出文字說明、證明過程或演算步驟．

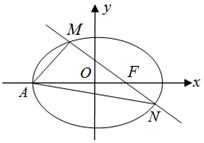• 21．如圖，已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左頂點A（-2，0），過右焦點F的直線l與橢圓C相交于M，N兩點，當直線l⊥x軸時，|MN|=3．
  （Ⅰ）求橢圓l的方程；
  （Ⅱ）記△AMF，△ANF的面積分別為S₁，S₂，求

  S

  1

  S

  2

  的取值范圍；
  （Ⅲ）若△AMN的重心在圓x²+y²=

  8

  49

  上，求直線l的斜率．
  組卷：221引用：2難度：0.6

  解析

• 22．已知函數f（x）=|e^x-

  a

  x

  |-alnx.
  （1）當a=-1時，求曲線y=f（x）在點（1，f（1））處的切線方程；
  （2）若f（x）＞a,求實數a的取值范圍．
  組卷：288引用：5難度：0.3

  解析