2022-2023學年浙江省七彩陽光聯盟高二（下）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知數列{a_n}的前n項和為S_n=n²，則a₇+a₈+a₉等于（　　）

  A．32

  B．45

  C．51

  D．56
  組卷：113引用：1難度：0.8

  解析

• 2．如果直線l₁：x+ty+1=0與直線l₂：tx+16y-4=0平行，那么實數t的值為（　　）

  A．4

  B．-4

  C．4或-4

  D．1或-4
  組卷：197引用：3難度：0.7

  解析

• 3．若曲線f（x）=e^x+sinx+m在x=0處的切線方程為2x-ny+1=0，則（　　）

  A．m=1，n=-1

  B．m=-1，n=1

  C．m=0，n=-1

  D．m=0，n=1
  組卷：72引用：3難度：0.7

  解析

• 4．等差數列{a_n}的公差不為0，其前n項和S_n滿足S_n≤S₁₀，則

  a

  1

  +

  a

  2

  +

  a

  3

  3

  a

  1

  的取值范圍為（　　）

  A． （ 8 9 ， 9 10 ）

  B． （ 9 10 ， 10 11 ）

  C． [ 8 9 ， 9 10 ]

  D． [ 9 10 ， 10 11 ]
  組卷：138引用：1難度：0.8

  解析

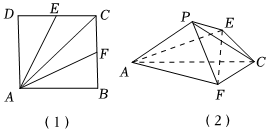• 5．若正方形ABCD的邊長為a,E，F分別為CD，CB的中點（如圖1），沿AE，AF將△ADE，△ABF折起，使得點B，D恰好重合于點P（如圖2），則直線PA與平面PCE所成角的正弦值為（　　）

  A． 2 2

  B． 3 4

  C． 3 6

  D． 3 2
  組卷：216引用：3難度：0.5

  解析

• 6．已知函數f（x）=2x-tlnx存在兩個零點，則實數t的取值范圍為（　　）

  A． （ e 2 ， + ∞ ）

  B．（e,+∞）

  C．（2e,+∞）

  D．（3e,+∞）
  組卷：215引用：5難度：0.5

  解析

• 7．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左、右焦點為F₁，F₂，過F₂的直線l分別交雙曲線C的左、右兩支于A、B．若|BF₁|：|AF₁|：|BF₂|=3：2：1，則雙曲線C的漸近線方程為（　　）

  A． y =± 3 6 4 x

  B． y =± 2 6 3 x

  C． y =± 2 3 3 x

  D． y =± 3 3 4 x
  組卷：149引用：2難度：0.5

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的離心率為

  5

  ，點P（2，2）在雙曲線C上．
  （1）求雙曲線C的方程；
  （2）若點A，B在雙曲線C的左、右兩支上，直線PA，PB均與圓O：

  x

  2

  +

  y

  2

  =

  r

  2

  （

  0

  ＜

  r

  ＜

  3

  ）

  相切，記直線PA，PB的斜率分別為k₁，k₂，△ABP的面積為S．
  ①k₁k₂是否為定值？如果是，求出這個定值；如果不是，請說明理由．
  ②已知圓O的面積為

  8

  5

  π，求S．
  組卷：75引用：1難度：0.5

  解析

• 22．已知函數f（x）=2xlnx-3e^x-2+1+（2a-5）x²，g（x）=axlnx+（a-3）x²+1，a∈R．
  （1）當a=2時，求函數g（x）的單調性；
  （2）若不等式f（x）≤g（x）對任意的x∈（0，+∞）恒成立，求a的取值范圍．
  組卷：98引用：1難度：0.3

  解析