2022-2023學年安徽省安慶二中八年級（上）期末數學試卷

一、選擇題（每小題4分，共40分）

• 1．如圖是科學防控新冠知識的圖片．其中的圖案是軸對稱圖形（　　）

  A．

  B．

  C．

  D．
  組卷：87引用：6難度：0.9

  解析

• 2．在平面直角坐標系中，下列各點在第二象限的是（　　）

  A．（-3，-2）

  B．（2，3）

  C．（3，-2）

  D．（-2，4）
  組卷：201引用：3難度：0.9

  解析

• 3．樂樂要從下面四組木棒中選擇一組制作一個三角形作品，你認為他應該選（　　）

  A．3，5，6

  B．2，3，5

  C．2，4，7

  D．3，8，4
  組卷：142引用：5難度：0.8

  解析

• 4．一次函數y=mx-m的圖象可能是（　　）

  A．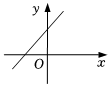

  B．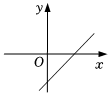

  C．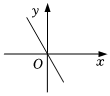

  D．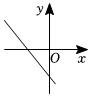
  組卷：1211引用：6難度：0.7

  解析

• 5．已知一個等腰三角形兩內角的度數之比為1：4，則這個等腰三角形頂角的度數為（　　）

  A．20°

  B．20°或120°

  C．36°
  組卷：435引用：3難度：0.5

  解析

• 6．已知點（-4，y₁），（2，y₂）都在直線y=

  -

  1

  2

  x+b上，則y₁，y₂大小關系是（　　）

  A．y1＞y2

  B．y1=y2

  C．y1＜y2

  D．不能比較
  組卷：107引用：3難度：0.6

  解析

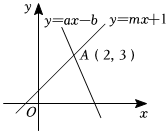• 7．如圖，直線y=ax-b與直線y=mx+1交于點A（2，3），則方程組

  ax - y = b ,

  mx - y = - 1

  解是（　　）

  A． x = 3 ， y = 2

  B． x = 2 ， y = 3

  C． x = - 3 ， y = - 2

  D． x = - 2 ， y = - 3
  組卷：197引用：4難度：0.6

  解析

三、解答題（共9小題．15-18每題8分，19-20每題10分，21-22每題12分，23題14分，共計60分）

• 22．已知三角形的三個內角分別為α、β、γ，當α是β的2倍時，我們稱此三角形為“特征三角形”，其中α稱為“特征角”．
  （1）已知一個“特征三角形”的“特征角”為100°，請直接寫出這個“特征三角形”的最小內角的度數為

  ．
  （2）是否存在“特征角”為120°的三角形，并說明理由；
  （3）如果一個特征三角形的三個內角滿足α≥γ≥β，求特征三角形中γ的取值范圍．
  組卷：122引用：3難度：0.3

  解析

• 23．（1）如圖1，在四邊形ABCD中，AB=AD，∠B=∠ADC=90°，點E、F分別在邊BC、CD上，且EF=BE+DF，探究圖中∠BAE、∠FAD、∠EAF之間的數量關系．
  小明探究的方法是：延長FD到點G，使DG=BE，連接AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結論，他的結論是

  ．
  （2）如圖2，在四邊形ABCD中，AB=AD，∠B+∠D=180°，點E、F分別在邊BC、CD上，且EF=BE+DF，探究上述結論是否仍然成立，并說明理由．
  （3）如圖3，在四邊形ABCD中，AB=AD，∠ABC+∠ADC=180°，若點E在CB的延長線上，點F在CD的延長線上，仍然滿足EF=BE+FD，請直接寫出∠EAF與∠DAB的數量關系為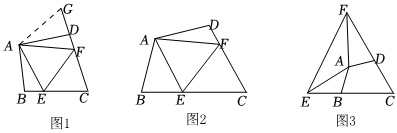

  ．
  
  組卷：181引用：2難度：0.1

  解析