2021-2022學(xué)年浙江省寧波外國語學(xué)校九年級（上）開學(xué)數(shù)學(xué)試卷

一．選擇題（24分）

• 1．若反比例函數(shù)

  y

  =

  k

  -

  1

  x

  的圖象位于第二、四象限，則k的取值可以是（　　）

  A．0

  B．1

  C．2

  D．以上都不是
  組卷：2182引用：82難度：0.9

  解析

• 2．已知關(guān)于x的一元二次方程mx²+2x-1=0有兩個不相等的實數(shù)根，則m的取值范圍是（　　）

  A．m＜-1

  B．m＞1

  C．m＜1且m≠0

  D．m＞-1且m≠0
  組卷：9229引用：77難度：0.9

  解析

• 3．有下列說法：①任意三點確定一個圓；②圓的兩條平行弦所夾的弧相等；③任意一個三角形有且僅有一個外接圓；④平分弦的直徑垂直于弦；⑤直徑是圓中最長的弦，其中錯誤的個數(shù)有（　　）

  A．2個

  B．3個

  C．4個

  D．5個
  組卷：338引用：2難度：0.6

  解析

• 4．在平面直角坐標(biāo)系中，將拋物線y=x²-4先向右平移兩個單位，再向上平移兩個單位，得到的拋物線的解析式是（　　）

  A．y=（x+2）2+2

  B．y=（x-2）2-2

  C．y=（x-2）2+2

  D．y=（x+2）2-2
  組卷：782引用：66難度：0.9

  解析

• 5．在⊙O中，如果

  ?

  AB

  =2

  ?

  CD

  ．那么弦AB與弦CD之間的關(guān)系是（　　）

  A．AB=2CD

  B．AB＞2CD

  C．AB＜2CD

  D．無法確定
  組卷：1014引用：4難度：0.9

  解析

• 6．如圖，一次函數(shù)y₁=k₁x+b的圖象和反比例函數(shù)y₂=

  k

  2

  x

  的圖象交于A（1，2），B（-2，-1）兩點，若y₁＜y₂，則x的取值范圍是（　　）

  A．x＜1	B．x＜-2
  C．-2＜x＜0或x＞1	D．x＜-2或0＜x＜1
  組卷：1531引用：69難度：0.7

  解析

• 7．已知點A（1，y₁）、B（

  -

  2

  ，

  y

  2

  ）、C（-2，y₃）在函數(shù)

  y

  =

  2

  （

  x

  +

  1

  ）

  2

  -

  1

  2

  上，則y₁、y₂、y₃的大小關(guān)系是（　　）

  A．y1＞y2＞y3

  B．y1＞y3＞y2

  C．y3＞y1＞y2

  D．y2＞y1＞y3
  組卷：1000引用：15難度：0.9

  解析

三、解答題（46分）

• 21．如圖，在平面直角坐標(biāo)系中，拋物線y=ax²+bx-4（a≠0）與x軸交于點A（-1，0），B（4，0），與y軸交于點C．
  （1）求該拋物線的解析式；
  （2）直線l為該拋物線的對稱軸，點D與點C關(guān)于直線l對稱，點P為直線AD下方拋物線上一動點，連接PA，PD，求△PAD面積的最大值．
  （3）在（2）的條件下，將拋物線y=ax²+bx-4（a≠0）沿射線AD平移4

  2

  個單位，得到新的拋物線y₁，點E為點P的對應(yīng)點，點F為y₁的對稱軸上任意一點，在y₁上確定一點G，使得以點D，E，F(xiàn)，G為頂點的四邊形是平行四邊形，寫出所有符合條件的點G的坐標(biāo)，并任選其中一個點的坐標(biāo)，寫出求解過程．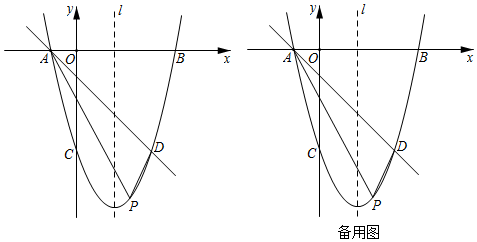
  
  組卷：3339引用：11難度：0.3

  解析

• 22．如圖1，將兩個完全相同的三角形紙片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．
  （1）操作發(fā)現(xiàn)：
  如圖2，固定△ABC，使△DEC繞點C旋轉(zhuǎn)，當(dāng)點D恰好落在AB邊上時，填空：
  ①線段DE與AC的位置關(guān)系是

  ；
  ②設(shè)△BDC的面積為S₁，△AEC的面積為S₂，則S₁與S₂的數(shù)量關(guān)系是

  ．
  （2）猜想論證：
  當(dāng)△DEC繞點C旋轉(zhuǎn)到如圖3所示的位置時，小明猜想（1）中S₁與S₂的數(shù)量關(guān)系仍然成立，并嘗試分別作出了△BDC和△AEC中BC、CE邊上的高，請你證明小明的猜想．
  （3）拓展探究
  已知∠ABC=60°，點D是角平分線上一點，BD=CD=6，DE∥AB交BC于點E（如圖4），若在射線BA上存在點F，使S_△DCF=S_△BDE，請求出相應(yīng)的BF的長．
  
  組卷：1190引用：6難度：0.1

  解析