2021-2022學年重慶實驗外國語學校九年級（上）入學數學試卷

一、選擇題：（本大共12小題，每小題4分，共48分）在每個小題的下面，都給出了代號為A、B、C、D的四個答案，其中只有一個是正的，請將答題卡上號右側正確答案所對應的方框涂黑.

• 1．下列既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．

  B．

  C．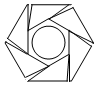

  D．
  組卷：61引用：2難度：0.8

  解析

• 2．將拋物線y=x²先向左平移3個單位再向下平移2個單位，得到新拋物線的表達式是（　　）

  A．y=（x+3）2+2

  B．y=（x+3）2-2

  C．y=（x-3）2+2

  D．y=（x-3）2-2
  組卷：112引用：7難度：0.8

  解析

• 3．已知⊙O的直徑是6，點O到直線l的距離為5，則直線l與⊙O的位置關系是（　　）

  A．相離

  B．相切

  C．相交

  D．無法判斷
  組卷：91引用：3難度：0.9

  解析

• 4．半徑為6，圓心角為60°的扇形面積為（　　）

  A．2π

  B．6π

  C．12π

  D．36π
  組卷：649引用：7難度：0.6

  解析

• 5．下列說法不正確的是（　　）

  A．平行四邊形兩組對邊分別平行

  B．平行四邊形的對角線互相平分

  C．平行四邊形的對角互補，鄰角相等

  D．平行四邊形的兩組對邊分別平行且相等
  組卷：1905引用：8難度：0.5

  解析

• 6．若x₁，x₂為拋物線y=2x²-5x-1與x軸相交的兩交點的橫坐標，則2x₁²-5x₁+3x₁x₂的值為（　　）

  A． 1 2

  B． 5 2

  C．- 1 2

  D．- 13 2
  組卷：1127引用：3難度：0.5

  解析

• 7．在同一平面直角坐標系中，函數y=mx+m和函數y=-mx²+2x+2（m是常數，且m≠0）的圖象可能是（　　）

  A．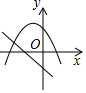

  B．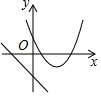

  C．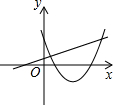

  D．
  組卷：737引用：6難度：0.9

  解析

• 8．某校初一年級開展了一班一特色活動，2001班以“地”為特色在學校的試驗園地進行種植蔬菜活動．試驗園的形狀是長15米、寬8米的矩形，為便于管理，要在中間開辟一橫兩縱共三條等寬的小道，使種植面積為110平方米，則小道的寬為多少米？若設小道的寬為x米，則根據題意，列方程為（　　）

  A．（15+2x）（8+x）=110	B．（15-2x）（8-x）=110
  C．（15+x）（8+2x）=110	D．（15-x）（8-2x）=110
  組卷：1625引用：8難度：0.6

  解析

三、（解答題：（本大題共8小題，19～25每題10分，26題8分，共78分）解答時每小題必須給出必要的演算過程或推理步驟，畫出必要的圖形（包括助線），請將解答過程書寫在答題卡中對應的位置上.

• 25．如圖，在平面直角坐標系中拋物線y=-x²+bx+c與y軸交于點C，與x軸交于A，B兩點（點A在點B的左側），直線BC的解析式為y=

  -

  1

  2

  x

  +

  2

  ．
  （1）求拋物線的解析式；
  （2）過點A作AD∥BC，交拋物線于點D，點E為直線BC上方拋物線上一動點，連接CE，EB，BD，DC．求四邊形BECD面積最大值時相應點E的坐標；
  （3）將拋物線y=-x²+bx+c向左平移2個單位，已知點M為拋物線y=-x²+bx+c的對稱軸上一動點，點N為平移后的拋物線上一動點．在（2）中當四邊形BECD的面積最大時，是否存在以A，E，M，N為頂點的四邊形為平行四邊形？若存在，直接寫出點N的坐標；若不存在，請說明理由．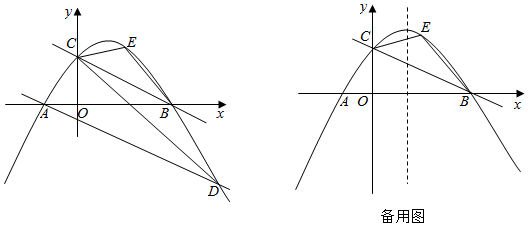
  
  組卷：643引用：1難度：0.3

  解析

• 26．如圖1，等腰△ABC中，AB=AC，D為AB上一點，等腰△CDE，CD=DE，∠BAC=∠EDC，DE交BC于點M，連接BE．
  （1）如圖1，若∠BAC=30°，AC=3，AD=

  3

  2

  ，求DE的長度；
  （2）如圖2，若DM⊥BC，求證：2MB+EB=BC；
  （3）如圖3，∠A=30°，AC∥DE，CN⊥AB，EF⊥CE，延長DB至點H，使得DH=DE，試判斷FM與FN的數量關系，并寫出證明過程．
  
  組卷：262引用：2難度：0.1

  解析