2022-2023學年上海市嘉定一中高二（下）期中數學試卷

一、填空題（本大題滿分48分，1—6每題4分，7—12每題5分）

• 1．在等比數列{a_n}中，若a₁=1，a₄=

  1

  64

  ，則公比q=

  ．
  組卷：65引用：1難度：0.8

  解析

• 2．拋物線y²=4x的焦點坐標是

  ．
  組卷：460引用：26難度：0.9

  解析

• 3．正方體ABCD-A₁B₁C₁D₁中，異面直線AB₁與BD所成角大小為

  ．
  組卷：49引用：2難度：0.7

  解析

• 4．邊長為2的正方形ABCD繞BC旋轉形成一個圓柱，則該圓柱的表面積為

  ．
  組卷：64引用：2難度：0.8

  解析

• 5．已知曲線f（x）=2x³-3x,過點（0，0）作曲線的切線，則切線方程

  ．
  組卷：73引用：1難度：0.6

  解析

• 6．“△ABC三個內角的度數構成等差數列”是“△ABC中有一個內角為60°”的

  條件．
  組卷：26引用：1難度：0.7

  解析

• 7．無窮等比數列{a_n}的通項公式a_n=（sinx）ⁿ，前n項的和為S_n，若

  lim

  n

  →

  +

  ∞

  S

  n

  =1，則滿足條件的x的取值的集合為

  ．
  組卷：37引用：1難度：0.6

  解析

三、解答題（本大題滿分36分）

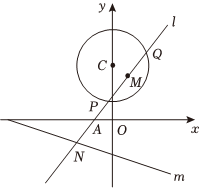• 20．已知過點A（-1，0）的直線l與圓C：x²+（y-3）²=4相交于P，Q兩點，M是弦PQ的中點；且直線l與直線m：x+3y+6=0相交于點N．
  （1）當直線l與直線m垂直時，求證：直線l經過圓心C；
  （2）當弦長|PQ|=2

  3

  時，求直線l的方程；
  （3）設t=

  AM

  ?

  AN

  ，試問t是否為定值，若為定值，請求出t的值；若不為定值，請說明理由．
  組卷：331引用：4難度：0.5

  解析

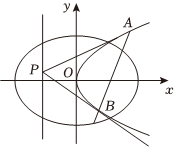• 21．已知橢圓C₁：

  x

  2

  3

  +

  y

  2

  2

  =1，以橢圓C₁的右焦點為焦點的拋物線C₂的頂點為原點，點P是拋物線C₂的準線上任意一點，過點P作拋物線C₂的兩條切線PA、PB，其中A、B為切點，設直線PA、PB的斜率分別為k₁，k₂．
  （1）求拋物線C₂的標準方程及其準線方程；
  （2）計算k₁?k₂的值；
  （3）求證：直線AB過定點，并求出這個定點的坐標；
  組卷：95引用：1難度：0.5

  解析