2023-2024學年北京市西城區鐵路二中高二（上）期中數學試卷

一、選擇題（每題5分，計50分）

• 1．直線

  3

  x-y+1=0的傾斜角的大小為（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：224引用：19難度：0.9

  解析

• 2．若a,b是異面直線，直線c∥a,則c與b的位置關系是（　　）

  A．相交

  B．異面

  C．平行

  D．異面或相交
  組卷：253引用：70難度：0.9

  解析

• 3．如圖在棱長為2的正方體ABCD-A₁B₁C₁D₁中，點E是AD的中點，那么異面直線D₁E和A₁B所成的角的余弦值等于（　　）

  A． 10 5

  B． 15 5

  C． 4 5

  D． 2 3
  組卷：226引用：3難度：0.7

  解析

• 4．過點A（-1，4）作圓（x-2）²+（y-3）²=4的切線，切點為B，則切線段AB長為（　　）

  A． 5

  B．3

  C． 6

  D． 7
  組卷：399引用：5難度：0.7

  解析

• 5．若點（k,0）與（b,0）的中點為（-3，0），則直線y=kx+b必定經過點（　　）

  A．（1，-6）

  B．（1，6）

  C．（-1，6）

  D．（-1，-6）
  組卷：67引用：3難度：0.7

  解析

• 6．已知

  MA

  ，

  MB

  是空間兩個不共線的向量，

  MC

  =

  5

  MA

  -

  3

  MB

  ，那么必有（　　）

  A． MA ， MC 共線	B． MB ， MC 共線
  C． MA ， MB ， MC 共面	D． MA ， MB ， MC 不共面
  組卷：167引用：3難度：0.8

  解析

• 7．點（1，2）關于直線x-2y-2=0的對稱點坐標是（　　）

  A．（-1，-4）

  B．（3，-2）

  C．（0，4）

  D．（-1，6）
  組卷：214引用：3難度：0.7

  解析

三、解答題（共5個大題，共計70分）

• 20．如圖，在多面體ABCDEF中，平面ADEF⊥平面ABCD，四邊形ADEF為正方形，四邊形ABCD為梯形，且AD∥BC，∠BAD=90°，AB=AD=1，BC=3．
  （Ⅰ）求證：AF⊥CD；
  （Ⅱ）求直線BF與平面CDE所成角的正弦值；
  （Ⅲ）線段BD上是否存在點M，使得直線CE∥平面AFM？若存在，求

  BM

  BD

  的值；若不存在，請說明理由．
  組卷：425引用：7難度：0.6

  解析

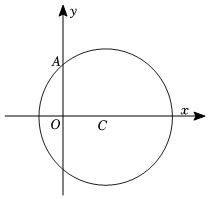• 21．已知圓C的圓心坐標為C（3，0），且該圓經過點A（0，4）．
  （1）求圓C的標準方程；
  （2）若點B也在圓C上，且弦AB長為8，求直線AB的方程；
  （3）直線l交圓C于M，N兩點，若直線AM，AN的斜率之積為2，求證：直線l過一個定點，并求出該定點坐標．
  組卷：246引用：8難度：0.4

  解析