當前位置：試卷中心 > 試卷詳情

2021-2022學年重慶市萬州第二高級中學高二（下）入學數學試卷

發布：2025/1/3 23:0:2

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知等比數列{a_n}的前n項和為S_n，若公比q=2，則
a
2
+
a
4
+
a
6
S
6
=（　　）
A．
2
3
B．
1
7
C．
1
3
D．
3
7
組卷：167引用：2難度：0.8
解析
2．已知
a
=（2，-1，3），
b
=（-1，4，-2），
c
=（1，3，λ），若
a
，
b
，
c
三向量共面，則實數λ等于（　　）
A．1 B．2 C．3 D．4
組卷：459引用：72難度：0.7
解析
3．已知直線l：x+y-1=0，則下列結論正確的是（　　）
A．直線l的傾斜角為
π
4
B．向量
v
=（1，1）是直線l的一個方向向量
C．過點（1，3）與直線l平行的直線方程為x+y+4=0
D．若直線m：x-y+1=0，則l⊥m
組卷：120引用：4難度：0.8
解析
4．已知雙曲線
x
2
a
2
-
y
2
b
2
=
1
的左、右焦點分別為F₁，F₂，P為雙曲線C上一點，PF₂⊥F₁F₂，直線PF₁與y軸交于點Q，若
|
OQ
|
=
b
4
，則雙曲線C的漸近線方程為（　　）
A．
y
=±
1
2
x
B．y=±2x C．
y
=±
1
4
x
D．y=±4x
組卷：43引用：2難度：0.6
解析
5．南宋數學家楊輝在《詳解九章算法》和《算法通變本末》中，提出了一些新的垛積公式，所討論的高階等差數列與一般的等差數列不同，前后兩項之差并不相等，但是逐項差數之差或者高次差成等差數列，如數列1，3，6，10，前后兩項之差組成新數列2，3，4，新數列2，3，4為等差數列，這樣的數列稱為二階等差數列．現有二階等差數列，其前7項分別為2，3，5，8，12，17，23，則該數列的第100項為（　　）
A．4862 B．4962 C．4952 D．4852
組卷：178引用：3難度：0.8
解析
6．數列{a_n}的前n項和為
S
n
，
S
n
=
1
2
（
a
n
+
1
a
n
）
（
n
∈
N
*
）
（a_n＞0），則下列選項中正確的是（　　）
A．
a
2021
≥
2
2021
B．
a
2021
≤
-
2
2021
C．a₂₀₂₁?a₂₀₂₂＞1 D．a₂₀₂₀?a₂₀₂₁＜1
組卷：87引用：2難度：0.5
解析
7．方程
1
-
x
2
=
kx
+
2
有兩個不同的解，則實數k的取值范圍為（　　）
A．
（
-
3
，
3
）
B．
（
-
∞
，-
3
）
∪
（
3
，
+
∞
）
C．
[
-
2
，-
3
）
∪
（
3
，
2
]
D．
（
-
2
，-
3
）
∪
（
3
，
2
）
組卷：97引用：3難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解算題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

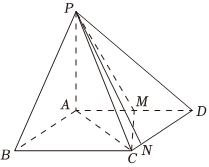21．如圖所示，在四棱錐P-ABCD中，四邊形ABCD是平行四邊形，AB=2
3
，BC=2，∠ABC=30°，PA⊥平面ABCD，PA=2
2
，點M在線段AD上，且AM=a,tan∠PMA=2
2
．
（1）求實數a的值；
（2）求平面MPC與平面APC夾角的余弦值；
（3）若點N是直線CD上的動點，求△NPB面積的最小值，并說明此時點N的位置．
組卷：158引用：3難度：0.4
解析
22．已知橢圓M：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的一個焦點與短軸的兩端點組成一個正三角形的三個頂點，且橢圓經過點
N
（
2
，
2
2
）
．
（1）求橢圓M的方程；
（2）若直線y=kx+m（k≠0）與圓E：x²+y²=
3
4
相切于點P，且交橢圓M于A，B兩點，射線OP于橢圓M交于點Q，設△OAB的面積與△QAB的面積分別為S₁，S₂．
①求S₁的最大值；
②當S₁取得最大值時，求
S
1
S
2
的值．
組卷：168引用：6難度：0.4
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A． a 2021 ≥ 2 2021	B． a 2021 ≤ - 2 2021
C．a₂₀₂₁?a₂₀₂₂＞1	D．a₂₀₂₀?a₂₀₂₁＜1

A．（ - 3 ， 3 ）	B．（ - ∞ ，- 3 ） ∪ （ 3 ， + ∞ ）
C． [ - 2 ，- 3 ） ∪ （ 3 ， 2 ]	D．（ - 2 ，- 3 ） ∪ （ 3 ， 2 ）

2021-2022學年重慶市萬州第二高級中學高二（下）入學數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知等比數列{an}的前n項和為Sn，若公比q=2，則a2+a4+a6S6=（ ）

2．已知a=（2，-1，3），b=（-1，4，-2），c=（1，3，λ），若a，b，c三向量共面，則實數λ等于（ ）

3．已知直線l：x+y-1=0，則下列結論正確的是（ ）

4．已知雙曲線x2a2-y2b2=1的左、右焦點分別為F1，F2，P為雙曲線C上一點，PF2⊥F1F2，直線PF1與y軸交于點Q，若|OQ|=b4，則雙曲線C的漸近線方程為（ ）

6．數列{an}的前n項和為Sn，Sn=12（an+1an）（n∈N*）（an＞0），則下列選項中正確的是（ ）

7．方程1-x2=kx+2有兩個不同的解，則實數k的取值范圍為（ ）

四、解算題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

1．已知等比數列{a_n}的前n項和為S_n，若公比q=2，則
a
2
+
a
4
+
a
6
S
6
=（　　）

2．已知
a
=（2，-1，3），
b
=（-1，4，-2），
c
=（1，3，λ），若
a
，
b
，
c
三向量共面，則實數λ等于（　　）

3．已知直線l：x+y-1=0，則下列結論正確的是（　　）

4．已知雙曲線
x
2
a
2
-
y
2
b
2
=
1
的左、右焦點分別為F₁，F₂，P為雙曲線C上一點，PF₂⊥F₁F₂，直線PF₁與y軸交于點Q，若
|
OQ
|
=
b
4
，則雙曲線C的漸近線方程為（　　）

6．數列{a_n}的前n項和為
S
n
，
S
n
=
1
2
（
a
n
+
1
a
n
）
（
n
∈
N
*
）
（a_n＞0），則下列選項中正確的是（　　）

7．方程
1
-
x
2
=
kx
+
2
有兩個不同的解，則實數k的取值范圍為（　　）