2023-2024學年北京市海淀區八一學校高三（上）開學數學試卷

一、選擇題共10小題，每小題4分，共40分.在每題列出的四個選項中，選出符合題目要求的一項.

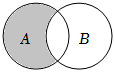• 1．若集合A={1，2，3，4，5}，集合B={x|x（4-x）＜0}，則圖中陰影部分表示（　　）

  A．{1，2，3，4}

  B．{1，2，3}

  C．{4，5}

  D．{1，4}
  組卷：186引用：11難度：0.9

  解析

• 2．設z=1+i,則z²-i=（　　）

  A．i

  B．-i

  C．1

  D．-1
  組卷：165引用：6難度：0.8

  解析

• 3．下列函數中，值域為（1，+∞）的是（　　）

  A．y=2x+1

  B． y = 1 x + 1

  C．y=log2|x|

  D．y=x2+1
  組卷：425引用：4難度：0.9

  解析

• 4．“m＞2”是“方程

  x

  2

  2

  -

  m

  +

  y

  2

  m

  +

  1

  =

  1

  表示雙曲線”的（　　）條件．

  A．必要不充分條件	B．充分不必要條件
  C．充要條件	D．既不充分也不必要條件
  組卷：142引用：5難度：0.7

  解析

• 5．埃及胡夫金字塔是世界古代建筑奇跡之一，它的形狀可視為一個正四棱錐，其側面與底面所成角的余弦值為

  5

  -

  1

  2

  ，則側面三角形的頂角的正切值為（　　）

  A．2

  B．3

  C． 5 - 1 2

  D． 5 + 1 2
  組卷：345引用：5難度：0.6

  解析

• 6．直線l經過點A（0，b），且與直線y=2x平行，如果直線l與曲線y=x²相切，那么b等于（　　）

  A． - 1 4

  B．-1

  C．1

  D． 1 2
  組卷：62引用：1難度：0.6

  解析

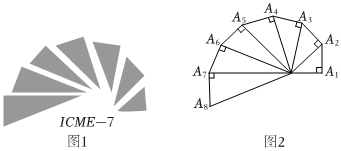• 7．圖1是第七屆國際數學教育大會的會徽圖案，會徽的主體圖案是由如圖2所示的一連串直角三角形演化而成的，其中OA₁=A₁A₂=A₂A₃=…=A₇A₈=1，如果把圖2中的直角三角形繼續作下去，記OA₁，OA₂，…，OA_n的長度構成的數列為{a_n}，則a₃₆+a₁₆=（　　）

  A．52

  B． 2 13

  C．10

  D．100
  組卷：86引用：2難度：0.8

  解析

三、解答題（本大題共6小題，共85分。解答應寫出文字說明，證明過程或演算步驟）

• 20．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右頂點分別為A₁，A₂，上下頂點分別為B₁，B₂，四邊形A₁B₁A₂B₂的面積為4，且該四邊形內切圓的方程為

  x

  2

  +

  y

  2

  =

  4

  5

  ．
  （1）求橢圓C的方程；
  （2）直線l：y=kx+m（k,m均為常數）與橢圓C相交于M，N兩個不同的點（M，N異于A₁，A₂），若以MN為直徑的圓過橢圓C的右頂點A₂，試判斷直線l能否過定點？若能，求出該定點坐標；若不能，請說明理由．
  組卷：78引用：2難度：0.5

  解析

• 21．將m×n階數陣

  a 11 ， a 12 ，…， a 1 n

  a 21 ， a 22 ，…， a 2 n

  ? ? ? ?

  a m 1 ， a m 2 ，…， a mn

  記作{a_ij}_m×n（其中，當且僅當i=s,j=t時，a_ij=a_st）．如果對于任意的i=1，2，3，…，m,當j₁＜j₂時，都有

  a

  i

  j

  1

  ＜

  a

  i

  j

  2

  ，那么稱數陣{a_ij}_m×n具有性質A．
  （Ⅰ）寫出一個具有性質A的數陣{a_ij}_3×4，滿足以下三個條件：①a₁₁=4，②數列{a_1n}是公差為2的等差數列，③數列{a_m1}是公比為

  1

  2

  的等比數列；
  （Ⅱ）將一個具有性質A的數陣{a_ij}_m×n的每一列原有的各數按照從上到下遞增的順序排列，形成一個新的m×n階數陣，記作數陣{b_ij}_m×n．試判斷數陣{b_ij}_m×n是否具有性質A，并說明理由．
  組卷：63引用：2難度：0.6

  解析