2022年廣東省珠海市香洲區九洲中學中考數學三模試卷

一、選擇題（本大題10小題，每小題3分，共30分）

• 1．-|-5|=（　　）

  A．5

  B．- 1 5

  C．-5

  D． 1 5
  組卷：158引用：10難度：0.9

  解析

• 2．《長津湖之水門橋》以39.06億元的票房創造中國電影票房的新高，將39.06億用科學記數法表示為（　　）

  A．39.06×109

  B．3.906×109

  C．390.6×1010

  D．0.3906×108
  組卷：170引用：8難度：0.7

  解析

• 3．冬季奧林匹克運動會（簡稱冬奧會）是世界規模最大的冬季綜合性運動會，每四年舉辦一屆．第24屆冬奧會將于2022年2月4日在北京開幕．下列四個圖分別是四屆冬奧會圖標中的一部分，其中不是軸對稱圖形的為（　　）

  A．

  B．

  C．

  D．
  組卷：61引用：5難度：0.8

  解析

• 4．若方程x²-2x+m=0沒有實數根，則m的值可以是（　　）

  A．-1

  B．0

  C．1

  D． 3
  組卷：2170引用：49難度：0.6

  解析

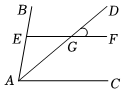• 5．如圖，AD平分∠BAC，點E在AB上，EF∥AC交AD于點G，若∠DGF=40°，則∠BEF的度數為（　　）

  A．20°

  B．40°

  C．50°

  D．80°
  組卷：83引用：3難度：0.7

  解析

• 6．《九章算術》中記載．“今有人共買物，人出八，盈三；人出七，不足四．問人數、物價各幾何？”其大意是：“現有一些人共同買一個物品，每人出8錢，還盈余3錢；每人出7錢，還差4錢，問人數、物品價格各是多少？”設人數為x人，物品的價格為y錢，根據題意，可列方程組為（　　）

  A． y = 8 x - 3 y = 7 x + 4	B． x = 8 y + 3 x = 7 y - 4
  C． y = 8 x + 3 y = 7 x - 4	D． x = 8 y - 3 x = 7 y + 4
  組卷：2344引用：22難度：0.5

  解析

• 7．不等式組

  x - 2 ＜ 0

  - x + 1 ＞ 0

  的解集為（　　）

  A．x＜1

  B．x≤2

  C．1＜x≤2

  D．無解
  組卷：80引用：1難度：0.6

  解析

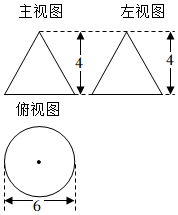• 8．如圖，是一個幾何體的三視圖，那么這個幾何體的側面積是（　　）

  A．12π

  B．15π

  C．20π

  D．25π
  組卷：311引用：3難度：0.7

  解析

五.解答題（本大題2小題，每小題10分，共20分）

• 24．如圖，矩形ABCD中，AB=3，BC=4，點P，Q分別在BC，CD上（均不含端點），且BP=CQ，PE⊥BD于點E，將PE平移得到QF，點P與點Q對應，設BP=x.
  
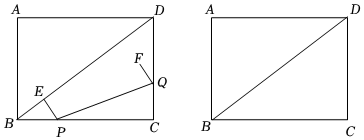
  計算BD=

  ；當x=1時，求QF的長．
  嘗試：（1）若∠EPQ=90°，求x的值；
  （2）當0＜x＜3時，求點F到BD的距離（用含x的式子表示）．
  探究：連接PF，若點P為BC的中點，直接寫出PF的長．
  組卷：195引用：3難度：0.3

  解析

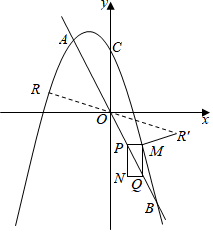• 25．如圖，二次函數y=-x²-2x+4-a²的圖象與一次函數y=-2x的圖象交于點A、B（點B在右側），與y軸交于點C，點A的橫坐標恰好為a.動點P、Q同時從原點O出發，沿射線OB分別以每秒

  5

  和2

  5

  個單位長度運動，經過t秒后，以PQ為對角線作矩形PMQN，且矩形四邊與坐標軸平行．
  （1）求a的值及t=1秒時點P的坐標；
  （2）當矩形PMQN與拋物線有公共點時，求時間t的取值范圍；
  （3）在位于x軸上方的拋物線圖象上任取一點R，作關于原點（0，0）的對稱點為R′，當點M恰在拋物線上時，求R′M長度的最小值，并求此時點R的坐標．
  組卷：2358引用：9難度：0.3

  解析