2023-2024學年浙江省臺州市高三（上）第一次質檢數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．設集合A={（1，2），（2，1）}，B={（x,y）|x-y=1}，則A∩B=（　　）

  A．{2，1}

  B．{（2，1）}

  C．{（1，2）}

  D．{1，2}
  組卷：682引用：11難度：0.7

  解析

• 2．若

  cosα

  =

  cos

  （

  π

  3

  +

  α

  ）

  ，則α的取值可以為（　　）

  A． π 6

  B． π 3

  C． 5 π 6

  D． 2 π 3
  組卷：42引用：2難度：0.7

  解析

• 3．已知非零向量

  a

  ，

  b

  ，

  c

  滿足

  |

  a

  |

  =

  |

  b

  |

  ，

  c

  =

  1

  3

  a

  ，若

  c

  為

  b

  在

  a

  上的投影向量，則向量

  a

  ，

  b

  夾角的余弦值為（　　）

  A． 1 2

  B． 1 3

  C． 1 4

  D． 1 5
  組卷：254引用：5難度：0.8

  解析

• 4．設α，β為兩個不同的平面，l,m為兩條不同的直線，且m⊥α，l∥β，則“l∥m”是“α⊥β”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：156引用：5難度：0.6

  解析

• 5．杭州第19屆亞運會火炬9月14日在浙江臺州傳遞，火炬傳遞路線以“和合臺州活力城市”為主題，全長8公里．從和合公園出發，途經臺州市圖書館、文化館、體育中心等地標建筑．假設某段線路由甲、乙等6人傳遞，每人傳遞一棒，且甲不從乙手中接棒，乙不從甲手中接棒，則不同的傳遞方案共有（　　）

  A．288種

  B．360種

  C．480種

  D．504種
  組卷：170引用：6難度：0.7

  解析

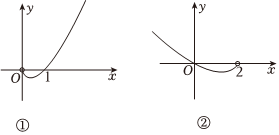• 6．函數y=f（x）的圖象如圖①所示，則如圖②所示的函數圖象所對應的函數解析式可能為（　　）

  A． y = f （ 1 - 1 2 x ）	B． y = - f （ 1 - 1 2 x ）
  C．y=f（4-2x）	D．y=-f（4-2x）
  組卷：79引用：6難度：0.6

  解析

• 7．已知二面角α-l-β的平面角為

  θ

  （

  0

  ＜

  θ

  ＜

  π

  2

  ）

  ，A∈α，B∈β，C∈l,D∈l,AB⊥l,AB與平面β所成角為

  π

  6

  ．記△ACD的面積為S₁，△BCD的面積為S₂，則

  S

  1

  S

  2

  的最小值為（　　）

  A．2

  B． 3

  C． 3 2

  D． 1 2
  組卷：37引用：1難度：0.4

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知橢圓Γ：

  x

  2

  a

  2

  +

  y

  2

  =

  1

  （

  a

  ＞

  1

  ）

  的上、下頂點分別為A，B，點Q在線段AB上運動（不含端點），點P（-1，0），直線PQ與橢圓交于C，D兩點（點C在點P左側），PD中點M的軌跡交y軸于E，F兩點，且|EF|=

  3

  2

  ．
  （Ⅰ）求橢圓Γ的方程；
  （Ⅱ）記直線AC，AD的斜率分別為k₁，k₂，求k₁-k₂的最小值．
  組卷：66引用：1難度：0.6

  解析

• 22．設

  f

  （

  x

  ）

  =

  x

  lnx

  ．
  （1）求證：

  f

  （

  x

  ）

  ＜

  x

  2

  x

  -

  1

  ；
  （2）若f（x）＜nln（1-x²）恒成立，求整數n的最大值．（參考數據ln2≈0.693，ln3≈1.099）
  
  組卷：48引用：2難度：0.6

  解析