當前位置：試卷中心 > 試卷詳情

2022-2023學年湖南省懷化市雅禮實驗學校高二（上）期中數學試卷

發布：2024/9/30 5:0:1

一、單選題

1．如圖所示的四個幾何體，其中判斷正確的是（　　）
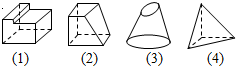
A．（1）不是棱柱 B．（2）是棱柱
C．（3）是圓臺 D．（4）是棱錐
組卷：135引用：2難度：0.9
解析
2．在四面體OABC中，點M在線段OA上，且OM=2MA，N為BC中點，已知
OA
=
a
，
OB
=
b
，
OC
=
c
，則
MN
等于（　　）
A．
1
2
a
-
2
3
b
+
1
2
c
B．
-
2
3
a
+
1
2
b
+
1
2
c
C．
1
2
a
+
1
2
b
-
1
2
c
D．
2
3
a
+
2
3
b
-
1
2
c
組卷：196引用：6難度：0.7
解析
3．已知向量
a
=
（
2
，-
3
，
0
）
，
b
=
（
0
，
3
，
4
）
，則向量
a
在向量
b
方向上的投影向量為（　　）
A．
-
9
13
a
B．
9
13
a
C．
9
25
b
D．
-
9
25
b
組卷：51引用：5難度：0.8
解析
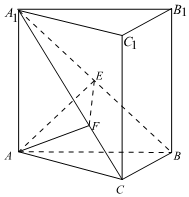4．《九章算術》中將底面為直角三角形且側棱垂直于底面的三棱柱稱為“塹堵”；底面為矩形，一條側棱垂直于底面的四棱錐稱之為“陽馬”；四個面均為直角三角形的四面體稱為“鱉臑”．如圖在塹堵ABC-A₁B₁C₁中，AC⊥BC，且AA₁=AB=2．下列說法錯誤的是（　　）
A．四棱錐B-A₁ACC₁為“陽馬”
B．四面體A₁C₁CB為“鱉臑”
C．四棱錐B-A₁ACC₁體積最大為
2
3
D．過A點分別作AE⊥A₁B于點E，AF⊥A₁C于點F，則EF⊥A₁B
組卷：172引用：13難度：0.8
解析
5．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點分別為F₁，F₂，P為橢圓C上一點，若△PF₁F₂的周長為54，且橢圓C的短軸長為18，則橢圓C的離心率為（　　）
A．
3
4
B．
4
5
C．
2
3
D．
2
2
5
組卷：235引用：4難度：0.7
解析
6．若一個圓錐的底面面積為π，其側面展開圖是圓心角為
2
π
3
的扇形，則該圓錐的體積為（　　）
A．
3
3
π
B．
2
2
3
π
C．
3
π
D．
2
3
π
組卷：307引用：14難度：0.7
解析
7．已知雙曲線
y
2
a
2
-
x
2
2
=
1
的兩個焦點分別為F₁、F₂，離心率等于
3
，設雙曲線的兩條漸近線分別為直線l₁、l₂；若點A、B分別在l₁、l₂上，且滿足
3
|
AB
|
=
2
|
F
1
F
2
|
，則線段AB的中點M的軌跡C的方程為（　　）
A．
x
2
4
+
y
2
=
1
B．
x
2
3
+
y
2
=
1
C．
x
2
6
+
y
2
=
1
D．
x
2
2
+
y
2
=
1
組卷：111引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題

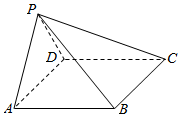21．如圖，在四棱錐P-ABCD中，AB∥CD，且∠BAP=∠CDP=90°．
（1）證明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC，∠APD=90°，求二面角A-PB-C的余弦值．
組卷：13315引用：38難度：0.6
解析
22．設橢圓
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的左焦點為F，上頂點為B．已知橢圓的短軸長為4，離心率為
5
5
．
（Ⅰ）求橢圓的方程；
（Ⅱ）設點P在橢圓上，且異于橢圓的上、下頂點，點M為直線PB與x軸的交點，點N在y軸的負半軸上．若|ON|=|OF|（O為原點），且OP⊥MN，求直線PB的斜率．
組卷：7977引用：17難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（1）不是棱柱	B．（2）是棱柱
C．（3）是圓臺	D．（4）是棱錐

A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c

2022-2023學年湖南省懷化市雅禮實驗學校高二（上）期中數學試卷

一、單選題

1．如圖所示的四個幾何體，其中判斷正確的是（ ）

2．在四面體OABC中，點M在線段OA上，且OM=2MA，N為BC中點，已知OA=a，OB=b，OC=c，則MN等于（ ）

3．已知向量a=（2，-3，0），b=（0，3，4），則向量a在向量b方向上的投影向量為（ ）

5．已知橢圓C：x2a2+y2b2=1（a＞b＞0）的左、右焦點分別為F1，F2，P為橢圓C上一點，若△PF1F2的周長為54，且橢圓C的短軸長為18，則橢圓C的離心率為（ ）

6．若一個圓錐的底面面積為π，其側面展開圖是圓心角為2π3的扇形，則該圓錐的體積為（ ）

7．已知雙曲線y2a2-x22=1的兩個焦點分別為F1、F2，離心率等于3，設雙曲線的兩條漸近線分別為直線l1、l2；若點A、B分別在l1、l2上，且滿足3|AB|=2|F1F2|，則線段AB的中點M的軌跡C的方程為（ ）

四、解答題

21．如圖，在四棱錐P-ABCD中，AB∥CD，且∠BAP=∠CDP=90°．（1）證明：平面PAB⊥平面PAD；（2）若PA=PD=AB=DC，∠APD=90°，求二面角A-PB-C的余弦值．

1．如圖所示的四個幾何體，其中判斷正確的是（　　）

2．在四面體OABC中，點M在線段OA上，且OM=2MA，N為BC中點，已知
OA
=
a
，
OB
=
b
，
OC
=
c
，則
MN
等于（　　）

3．已知向量
a
=
（
2
，-
3
，
0
）
，
b
=
（
0
，
3
，
4
）
，則向量
a
在向量
b
方向上的投影向量為（　　）

5．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點分別為F₁，F₂，P為橢圓C上一點，若△PF₁F₂的周長為54，且橢圓C的短軸長為18，則橢圓C的離心率為（　　）

6．若一個圓錐的底面面積為π，其側面展開圖是圓心角為
2
π
3
的扇形，則該圓錐的體積為（　　）

7．已知雙曲線
y
2
a
2
-
x
2
2
=
1
的兩個焦點分別為F₁、F₂，離心率等于
3
，設雙曲線的兩條漸近線分別為直線l₁、l₂；若點A、B分別在l₁、l₂上，且滿足
3
|
AB
|
=
2
|
F
1
F
2
|
，則線段AB的中點M的軌跡C的方程為（　　）

21．如圖，在四棱錐P-ABCD中，AB∥CD，且∠BAP=∠CDP=90°．
（1）證明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC，∠APD=90°，求二面角A-PB-C的余弦值．