2022-2023學年山東省青島二中高二（上）月考數學試卷（10月份）

一、解答題（共8小題，滿分40分）

• 1．直線

  3

  x+y-3=0的傾斜角為（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：119引用：13難度：0.8

  解析

• 2．已知△ABC中，

  a

  =

  6

  2

  ，b=1，

  A

  =

  π

  3

  ，則B=（　　）

  A． π 4 或 3 π 4

  B． π 4

  C． π 3 或 2 π 3

  D． π 3
  組卷：136引用：1難度：0.7

  解析

• 3．設a∈R，則“

  a

  =

  1

  2

  ”是“直線x+2ay+3=0與直線2ax+y-1=0平行”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：86引用：2難度：0.8

  解析

• 4．已知

  cos

  （

  π

  6

  -

  α

  ）

  =

  4

  5

  ，則

  sin

  （

  α

  +

  π

  3

  ）

  =（　　）

  A． ± 3 5

  B． 3 5

  C． - 3 5

  D． 4 5
  組卷：319引用：1難度：0.8

  解析

• 5．已知非零向量

  a

  ，

  b

  滿足

  |

  b

  |

  =

  2

  |

  a

  |

  ，且

  （

  a

  -

  b

  ）

  ⊥

  a

  ，則

  a

  -

  b

  與

  b

  的夾角為（　　）

  A． 2 π 3

  B． π 3

  C． 5 π 6

  D． π 6
  組卷：139引用：1難度：0.7

  解析

• 6．已知圓錐的高為

  3

  ，底面半徑為3，則過此圓錐頂點的截面面積的最大值為（　　）

  A． 3 3 2

  B． 3 3

  C．4

  D．6
  組卷：74引用：1難度：0.7

  解析

• 7．在空間直角坐標系O-xyz中，正四面體P-ABC的頂點A、B分別在x軸，y軸上移動．若該正四面體的棱長是4，則|OP|的取值范圍是（　　）

  A．[2，6]

  B． [ 2 3 - 2 ， 2 3 + 2 ]

  C． [ 2 3 - 2 ， 4 ]

  D． [ 2 ， 2 3 + 2 ]
  組卷：46引用：2難度：0.6

  解析

四、解答題。（共6小題，滿分70分）

• 21．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分圖像如圖所示．
  （1）求f（x）的解析式及對稱中心；
  （2）若

  f

  （

  α

  2

  ）

  =

  4

  3

  ，求

  cos

  （

  2

  α

  +

  π

  3

  ）

  值；
  （3）先將f（x）的圖像橫坐標不變，縱坐標縮短到原來的

  1

  2

  倍，得到函數g（x）圖像，再向g（x）圖像右平移

  π

  12

  個單位后得到h（x）的圖像，求函數y=h（x）在

  x

  ∈

  [

  π

  12

  ，

  3

  π

  4

  ]

  上的單調減區間．
  組卷：185引用：1難度：0.5

  解析

• 22．如圖，四邊形ABCD為梯形，AB∥CD，∠C=60°，CD=2CB=4AB=4，點E在線段CD上，且BE⊥CD．現將△ADE沿AE翻折到△PAE的位置，使得

  PC

  =

  10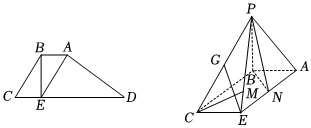

  ．
  
  （1）取PC中點G，AE中點N，證明EG∥平面PBN；
  （2）證明：AE⊥PB；
  （3）點M是線段PE上的一點（不包含端點），是否存在點M，使得二面角P-BC-M的余弦值為

  6

  3

  ？若存在，則求出

  ME

  PE

  ；若不存在，請說明理由．
  組卷：136引用：1難度：0.4

  解析