2022-2023學年福建省泉州市永春二中、平山中學等五校高二（下）期中數學試卷

一、單選題（本大題共8個小題，每小題5分，共40分，每小題均有四個選項，其中只有一項符合題目要求）

• 1．某高校有4名志愿者參加社區志愿工作，若每天早、中晚三班，每班1人，每人每天最多值一班，則值班當天不同的排班種類為（　　）

  A．12

  B．18

  C．24

  D．144
  組卷：51引用：3難度：0.7

  解析

• 2．已知函數f（x）=e^x-1+f′（1）x²+x+1，則f′（2）=（　　）

  A．e+2

  B．e-3

  C．e-5

  D．e-7
  組卷：184引用：4難度：0.7

  解析

• 3．若

  C

  2

  n

  +

  A

  2

  n

  =

  30

  ，則n的值為（　　）

  A．4

  B．5

  C．6

  D．7
  組卷：171引用：5難度：0.7

  解析

• 4．若

  （

  3

  -

  x

  ）

  （

  1

  +

  x

  ）

  10

  =

  a

  0

  +

  a

  1

  x

  +

  …

  +

  a

  11

  x

  11

  ，x∈R，則

  a

  1

  ?

  3

  +

  a

  2

  ?

  3

  2

  +

  …

  +

  a

  11

  ?

  3

  11

  的值為（　　）

  A．-3

  B．3

  C．39

  D．39-1
  組卷：115引用：2難度：0.8

  解析

• 5．設集合A={（x₁，x₂，x₃，x₄，x₅）|x_i∈{-1，0，1}，i=1，2，3，4，5}，那么集合A中滿足條件“1≤|x₁|+|x₂|+|x₃|+|x₄|+|x₅|≤3”的元素個數為（　　）

  A．60

  B．90

  C．120

  D．130
  組卷：2543引用：37難度：0.9

  解析

• 6．已知函數f（x）=

  1

  4

  x²+cosx,f'（x）是函數f（x）的導函數，則f'（x）的圖象大致是（　　）

  A．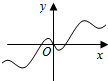

  B．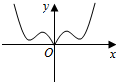

  C．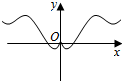

  D．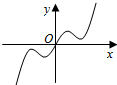
  組卷：74引用：7難度：0.7

  解析

• 7．北京2022年冬奧會的吉祥物冰墩墩和雪容融非常可愛，某教師用吉祥物的小掛件作為獎品鼓勵學生學習，設計獎勵方案如下：在不透明的盒子中放有大小、形狀完全相同的6張卡片，上面分別標有編號1，2，3，4，5，6，現從中不放回地抽取兩次卡片，每次抽取一張，只要抽到的卡片編號大于4就可以中獎，已知第一次抽到卡片中獎，則第二次抽到卡片中獎的概率為（　　）

  A． 1 15

  B． 1 5

  C． 1 3

  D． 2 5
  組卷：46引用：3難度：0.7

  解析

四、解答題（本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟）

• 21．某學校組織“一帶一路”知識競賽，有A，B兩類問題．每位參加比賽的同學先在兩類問題中選擇一類并從中隨機抽取一個問題回答，若回答錯誤則該同學比賽結束；若回答正確則從另一類問題中再隨機抽取一個問題回答，無論回答正確與否，該同學比賽結束．A類問題中的每個問題回答正確得20分，否則得0分；B類問題中的每個問題回答正確得80分，否則得0分．
  已知小明能正確回答A類問題的概率為0.8，能正確回答B類問題的概率為0.6，且能正確回答問題的概率與回答次序無關．
  （1）若小明先回答A類問題，記X為小明的累計得分，求X的分布列；
  （2）為使累計得分的期望最大，小明應選擇先回答哪類問題？并說明理由．
  組卷：8197引用：21難度：0.6

  解析

• 22．已知函數f（x）=xlnx-

  1

  2

  x²+（2a-1）x（a∈R）．
  （1）討論函數f（x）的極值點的個數；
  （2）已知函數g（x）=

  e

  x

  x

  -f′（x）有兩個不同的零點x₁，x₂，且x₁＜x₂.證明：x₂-x₁＜

  4

  a

  2

  -

  2

  a

  -

  1

  2

  a

  -

  1

  ．
  組卷：696引用：4難度：0.1

  解析