2022-2023學年北京十二中高二（上）期末數學試卷

一.選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．一個袋中裝有大小、質地相同的3個紅球和3個黑球，從中隨機摸出3個球，設事件A=“至少有2個黑球”，下列事件中，與事件A互斥而不互為對立的是（　　）

  A．都是黑球	B．恰好有1個黑球
  C．恰好有1個紅球	D．至少有2個紅球
  組卷：560引用：7難度：0.8

  解析

• 2．若向量

  a

  =（1，-1，λ），

  b

  =（1，-2，1），

  c

  =（1，1，1），滿足條件（

  c

  -

  a

  ）?

  b

  =-1，則λ=（　　）

  A．-1

  B．-2

  C．1

  D．2
  組卷：320引用：1難度：0.7

  解析

• 3．橢圓2x²+y²=1的焦點坐標為（　　）

  A．F1（-1，0），F2（1，0）	B．F1（0，-1），F2（0，1）
  C． F 1 （ - 2 2 ， 0 ） ， F 2 （ 2 2 ， 0 ）	D． F 1 （ 0 ，- 2 2 ） ， F 2 （ 0 ， 2 2 ）
  組卷：254引用：1難度：0.7

  解析

• 4．為了解某地農村經濟情況，對該地農戶家庭年收入進行抽樣調查，將農戶家庭年收入的調查數據整理得到如下頻率分布直方圖：
  
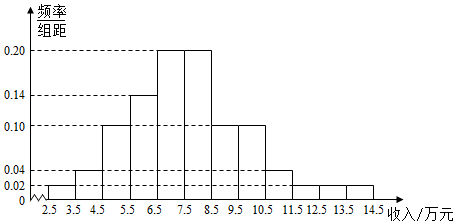
  根據此頻率分布直方圖，下面結論中不正確的是（　　）

  A．該地農戶家庭年收入低于4.5萬元的農戶比率估計為6%

  B．該地農戶家庭年收入不低于10.5萬元的農戶比率估計為10%

  C．估計該地農戶家庭年收入的平均值不超過6.5萬元

  D．估計該地有一半以上的農戶，其家庭年收入介于4.5萬元至8.5萬元之間
  組卷：4290引用：29難度：0.8

  解析

• 5．已知F₁，F₂是雙曲線

  x

  2

  4

  -

  y

  2

  6

  =

  1

  的兩個焦點，點P在雙曲線上，若|PF₁|=5，則|PF₂|=（　　）

  A．1或9

  B．3或7

  C．9

  D．7
  組卷：245引用：3難度：0.7

  解析

• 6．在空間直角坐標系中，已知三點O（0，0，0），A（1，2，1），B（1，-1，0），若點C在平面OAB內，則點C的坐標可能是（　　）

  A．（-1，-1，3）

  B．（3，0，1）

  C．（1，1，2）

  D．（1，-1，2）
  組卷：76引用：2難度：0.7

  解析

• 7．方程|x|-1=

  2

  y

  -

  y

  2

  表示的曲線為（　　）

  A．兩個半圓

  B．一個圓

  C．半個圓

  D．兩個圓
  組卷：1308引用：7難度：0.5

  解析

三、解答題：本大題共5小題，共60分．解答應寫出文字說明，演算步驟或證明過程．

• 22．已知橢圓W以坐標軸為對稱軸，且經過兩點A（2，0），B

  （

  1

  ，

  3

  2

  ）

  ，
  （Ⅰ）求橢圓W的方程；
  （Ⅱ）設過點P（2，1）的直線l交橢圓W于C、D兩點，過點D作垂直于x軸的直線，與線段AB交于點M，與AC交于點E，再從條件①、條件②、條件③中選擇一個作為已知．求

  |

  MD

  |

  |

  ME

  |

  的值．
  條件①：直線l的斜率為1；
  條件②：直線l過點B關于y軸的對稱點；
  條件③：直線l過坐標原點O．
  注：如果選擇條件①、條件②和條件③分別解答，按第一個解答計分．
  組卷：190引用：1難度：0.5

  解析

• 23．對于集合A，定義函數f_A（x）=

  1 ， x ? A ，

  - 1 ， x ∈ A .

  
  對于兩個集合A，B，定義運算A*B={x|f_A（x）?f_B（x）=-1}．
  （1）若A={1，2，3}，B={2，3，4，5}，寫出f_A（1）與f_B（1）的值，并求出A*B；
  （2）證明：f_A*B（x）=f_A（x）?f_B（x）；
  （3）證明：*運算具有交換律和結合律，即A*B=B*A，（A*B）*C=A*（B*C）．
  組卷：175引用：4難度：0.6

  解析