2022-2023學年貴州省貴陽一中高二（下）質檢數學試卷（四）

一、單項選擇題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．若集合A={x|ln（x-1）＜0}，B={x|2x-3≥0}，則A∩B=（　　）

  A．{x|1＜x＜2}

  B． { x | 3 2 ≤ x ＜ 2 }

  C． { x | x ≥ 3 2 }

  D．{x|x＞2}
  組卷：50引用：3難度：0.8

  解析

• 2．已知復數z滿足

  1

  +

  3

  i

  z

  =

  3

  +

  4

  i

  ，則

  |

  z

  |

  =（　　）

  A． 2 5 5

  B． 10 5

  C． 2 5

  D． 2 5
  組卷：76引用：5難度：0.8

  解析

• 3．近期，貴陽一中某社團開展了一次校內招新活動，甲、乙、丙三名同學都投遞了簡歷，三人簡歷通過的概率分別為0.8，0.8，0.7，則三人中至少有一人簡歷通過的概率為（　　）

  A．0.448

  B．0.948

  C．0.96

  D．0.988
  組卷：84引用：2難度：0.7

  解析

• 4．函數

  f

  （

  x

  ）

  =

  x

  e

  x

  +

  e

  -

  x

  的圖象大致為（　　）

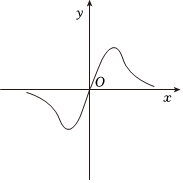
  A．	B．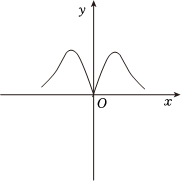
  C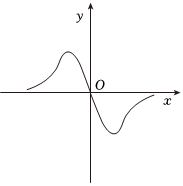．	D．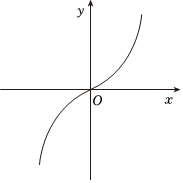
  組卷：277引用：11難度：0.7

  解析

• 5．已知向量

  a

  =

  （

  1

  ，

  3

  ）

  ，

  |

  b

  |

  =

  3

  ，

  ?

  a

  ，

  b

  ?

  =

  2

  π

  3

  ，則

  （

  3

  a

  -

  b

  ）

  ?

  （

  2

  a

  +

  b

  ）

  =（　　）

  A．30

  B．18

  C．12

  D．9
  組卷：51引用：2難度：0.7

  解析

• 6．過點（1，2）且垂直于直線3x-2y+5=0的直線方程為（　　）

  A．2x+3y-8=0

  B．2x-3y+4=0

  C．3x-2y+1=0

  D．2x+3y+8=0
  組卷：227引用：4難度：0.7

  解析

• 7．已知S_n為正項等比數列{a_n}的前n項和，a₁與S₃分別為方程x²-11x+28=0的兩個根．則S₄=（　　）

  A．7

  B．8

  C． 15 2

  D． 17 2
  組卷：43引用：2難度：0.7

  解析

四、解答題（共70分.解答應寫出文字說明，證明過程或演算步驟）

• 21．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  過點

  （

  1

  ，

  3

  2

  ）

  ，且焦距為

  2

  3

  ．
  （1）求橢圓C的標準方程；
  （2）若Q為x軸上一定點（m,0），過點Q的直線與橢圓交于A，B兩點，點B關于x軸的對稱點為B′（B′，A，B三點互異），直線AB′交x軸于點P，試探究|OP|?|OQ|是否為定值，若為定值，并求出該定值．
  組卷：16引用：2難度：0.5

  解析

• 22．給出定義：設f′（x）是函數y=f（x）的導函數，f″（x）是函數y=f′（x）的導函數，若方程f″（x）=0有實數解x₀，則稱（x₀，f（x₀））為函數y=f（x）的“固點”．經研究發現所有的三次函數f（x）=ax³+bx²+cx+d（a≠0）都有“固點”，且該“固點”也是函數y=f（x）的圖象的對稱中心．根據以上信息和相關知識回答下列問題：已知函數f（x）=x³+（3a-3）x²+（6a-9a²）x-5a（a∈R）．
  （1）當a=-1時，試求y=f（x）的對稱中心；
  （2）討論f（x）的單調性；
  （3）當a=2時，f（x）=m有三個不相等的實數根x₁＜x₂＜x₃，當|x₁-x₃|取得最大值時，求m的值．
  組卷：71引用：7難度：0.6

  解析