2023年陜西省西安建筑科技大學附中中考數學一模試卷

一、選擇題(共8小題，每小題3分，計24分，每小題只有一個選項是符合題意的)

• 1．2050的絕對值是（　　）

  A．2050

  B． 1 2050

  C．-2050

  D． - 1 2050
  組卷：50引用：1難度：0.7

  解析

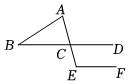• 2．如圖，已知直線BD∥EF，AE與BD交于點C，若∠B=30°20′，∠A=75°20'，則∠E的度是（　　）

  A．105°40′

  B．105°20′

  C．125°40′

  D．135°20′
  組卷：247引用：2難度：0.6

  解析

• 3．下列運算正確的是（　　）

  A．（a2）4=a6

  B．a2?a4=a6

  C．a2+a4=a6

  D．a2÷a4=a6
  組卷：364引用：5難度：0.7

  解析

• 4．如圖，在△ABC中，點D，E分別是AB，BC邊的中點，點F在DE的延長線上．添加一個條件，使得四邊形ADFC為平行四邊形，則這個條件可以是（　　）

  A．∠B=∠F

  B．DE=EF

  C．AC=CF

  D．AD=CF
  組卷：1531引用：15難度：0.5

  解析

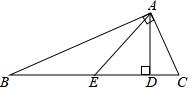• 5．如圖，在△ABC中，∠BAC=90°，AD⊥BC，垂足為D，E是邊BC的中點，AD=ED=3，則BC的長為（　　）

  A．3 2

  B．3 3

  C．6

  D．6 2
  組卷：1481引用：18難度：0.7

  解析

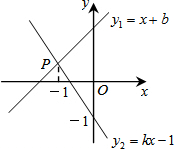• 6．如圖，直線y₁=x+b與y₂=kx-1相交于點P，若點P的橫坐標為-1，則關于x的不等式x+b＞kx-1的解集是（　　）

  A．x≥-1

  B．x＞-1

  C．x≤-1

  D．x＜-1
  組卷：8265引用：32難度：0.7

  解析

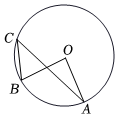• 7．如圖，OA，OB是⊙O的兩條半徑，點C在⊙O上，若∠AOB=80°，則∠C的度數為（　　）

  A．30°

  B．40°

  C．50°

  D．60°
  組卷：1959引用：29難度：0.7

  解析

• 8．已知二次函數y=ax²+2ax+3a²+3（其中x是自變量），當x≥2時，y隨x的增大而增大，且-2≤x≤1時，y的最大值為9，則a的值為（　　）

  A．1或-2

  B． - 2 或 2

  C． 2

  D．1
  組卷：9006引用：33難度：0.7

  解析

三、解答題（共13小題，計81分，解答應寫出過程）

• 25．二次函數y=ax²+bx+2的圖象交x軸于A（-1，0），B（4，0）兩點，交y軸于點C，動點M從點A出發(fā)，以每秒2個單位長度的速度沿AB方向運動，過點M作MN⊥x軸交直線BC于點N，交拋物線于點D，連接AC，設運動的時間為t秒．
  （1）求二次函數y=ax²+bx+2的表達式；
  （2）在直線MN上存在一點P，當△PBC是以∠BPC為直角的等腰直角三角形時，求此時點D的坐標．
  組卷：337引用：1難度：0.1

  解析

• 26．問題提出
  （1）如圖①，已知△ABC，試確定一點D，使得以A、B、C、D為頂點的四邊形為平行四邊形，請畫出這個平行四邊形；
  問題探究
  （2）如圖②，在矩形ABCD中，AB=4，BC=10，若要在該矩形中作一個面積最大的△BPC，且使∠BPC=90°，求滿足條件的點P到點A的距離；
  問題解決
  （3）如圖③，有一座塔A，按規(guī)劃，要以塔A為對稱中心，建一個面積盡可能大的形狀為平行四邊形的景區(qū)BCDE，根據實際情況，要求頂點B是定點，點B到塔A的距離為50m,∠CBE=120°，那么，是否可以建一個滿足要求的面積最大的平行四邊形景區(qū)BCDE？若可以，求出滿足要求的平行四邊形BCDE的最大面積；若不可以，請說明理由．（塔A的占地面積忽略不計）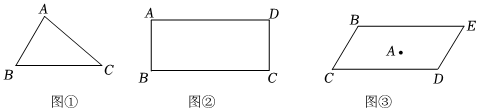
  
  組卷：136引用：1難度：0.1

  解析