2020-2021學年廣東省廣州五中高二（上）周測數學試卷（10.12）

一、單選題（每題5分，共40分）

• 1．傾斜角為120°，在x軸上的截距為-1的直線方程是（　　）

  A． 3 x + y + 1 = 0

  B． 3 x - y - 1 = 0

  C． 3 x + y - 3 = 0

  D． 3 x + y + 3 = 0
  組卷：551引用：3難度：0.5

  解析

• 2．“a=-1”是“直線ax+（2a-1）y+1=0和直線3x+ay+3=0垂直”的（　　）

  A．充分不必要的條件	B．必要不充分的條件
  C．充要條件	D．既不充分又不必要條件
  組卷：259引用：24難度：0.9

  解析

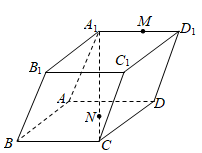• 3．如圖所示，在平行六面體ABCD-A₁B₁C₁D₁中，

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，M是A₁D₁的中點，點N是CA₁上的點，且CN：NA₁=1：4．用

  a

  ，

  b

  ，

  c

  表示向量

  MN

  的結果是（　　）

  A． 1 2 a + b + c	B． 1 5 a + 1 5 b + 4 5 c
  C． 1 5 a - 3 10 b - 1 5 c	D． 4 5 a + 3 10 b - 4 5 c
  組卷：809引用：10難度：0.9

  解析

• 4．已知空間向量

  a

  ，

  b

  ，

  c

  滿足

  a

  +

  b

  +

  c

  =

  0

  ，

  |

  a

  |

  =

  1

  ，

  |

  b

  |

  =

  2

  ，

  |

  c

  |

  =

  7

  ，則

  a

  與

  b

  的夾角為（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  組卷：451引用：14難度：0.6

  解析

• 5．過點（1，2），且與原點距離最大的直線方程是（　　）

  A．x+2y-5=0

  B．2x+y-4=0

  C．x+3y-7=0

  D．x-2y+3=0
  組卷：817引用：15難度：0.9

  解析

• 6．若向量

  a

  =（1，λ，2），

  b

  =（2，-1，2），

  c

  =（1，10，4），且

  a

  ，

  b

  ，

  c

  共面，則λ=（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：51引用：2難度：0.8

  解析

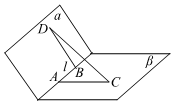• 7．如圖，二面角α-l-β等于120°，A、B是棱l上兩點，BD、AC分別在半平面α、β內，AC⊥l,BD⊥l,且2AB=AC=BD=2，則CD的長等于（　　）

  A． 2 3

  B． 13

  C．4

  D．5
  組卷：236引用：4難度：0.6

  解析

四、解答題（每題10分，共50分）

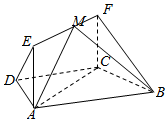• 20．如圖，在梯形ABCD中，AB∥CD，

  ∠

  BCD

  =

  2

  π

  3

  ，四邊形ACFE為矩形，且CF⊥平面ABCD，AD=CD=BC=CF=1．
  （1）求證：EF⊥平面BCF；
  （2）點M在線段EF（含端點）上運動，當點M在什么位置時，平面MAB與平面FCB所成銳二面角最大，并求此時二面角的余弦值．
  組卷：377引用：11難度：0.5

  解析

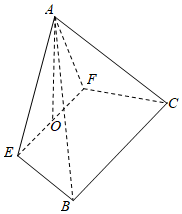• 21．如圖，將邊長為4的等邊三角形ABC沿與邊BC平行的直線EF折起，使得平面AEF⊥平面BCEF，O為EF的中點．
  （1）求平面AEF與平面AEB所成角的余弦值；
  （2）若BE⊥平面AOC，試求折痕EF的長；
  （3）當點O到平面ABC距離最大時，求折痕EF的長．
  組卷：273引用：5難度：0.3

  解析