當前位置：試卷中心 > 試卷詳情

2022-2023學年河南省周口恒大中學高一（下）月考數(shù)學試卷（5月份）

發(fā)布：2024/5/17 8:0:8

1．若a=2^0.5，b=log₃2，c=log₂0.2，則（　　）
A．a(chǎn)＞b＞c B．b＞a＞c C．c＞a＞b D．b＞c＞a
組卷：122引用：3難度：0.8
解析
2．已知函數(shù)
f
（
x
）
=
sin
（
ωx
-
π
3
）
（
ω
＞
0
）
，x∈[0，π]的值域為
[
-
3
2
，
1
]
，則ω的取值范圍是（　　）
A．
[
1
3
，
5
3
]
B．
[
5
6
，
1
]
C．
[
5
6
，
5
3
]
D．（0，+∞）
組卷：295引用：11難度：0.8
解析
3．
co
s
2
π
12
-
co
s
2
5
π
12
等于（　　）
A．
1
2
B．
3
3
C．
2
2
D．
3
2
組卷：281引用：10難度：0.8
解析
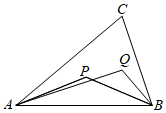4．如圖，設P、Q為△ABC內(nèi)的兩點，且
AP
=
2
5
AB
+
1
5
AC
，
AQ
=
2
3
AB
+
1
4
AC
，則△ABP的面積與△ABQ的面積之比為（　　）
A．
1
5
B．
4
5
C．
1
4
D．
1
3
組卷：416引用：22難度：0.9
解析
5．若（x+3i）²是純虛數(shù)（其中i為虛數(shù)單位），則實數(shù)x=（　　）
A．3 B．±1 C．-1 D．±3
組卷：6引用：3難度：0.8
解析
6．設函數(shù)
f
（
x
）
=
（
x
+
1
）
2
，
x
＜
1
4
-
x
-
1
，
x
≥
1
則使得f（-1）+f（m-1）=1成立的m的值為（　　）
A．10 B．0，-2 C．0，-2，10 D．1，-1，11
組卷：28引用：2難度：0.9
解析
7．下列關系正確的是（　　）
A．
2
∈
N
B．-1∈N C．
1
2
∈
N
D．0∈N
組卷：851引用：1難度：0.9
解析

21．設函數(shù)f_k（x）=2^x+（k-1）?2^-x（x∈R，k∈Z）．
（1）若f_k（x）是偶函數(shù)，求實數(shù)k的值；
（2）若存在x∈[1，2]，使得f₀（x）+mf₁（x）≤4成立，求實數(shù)m的取值范圍．
組卷：73引用：2難度：0.3
解析
22．定義在非零實數(shù)集上的函數(shù)f（x）對任意非零實數(shù)x,y都滿足
f
（
x
y
）
+
2
f
（
y
x
）
=
2
x
-
y
x
．
（1）求f（2）的值；
（2）求f（x）的解析式；
（3）設函數(shù)g（x）=xf（x），求g（x）在區(qū)間
[
1
4
，
2
m
]
上的最大值h（m）．
組卷：75引用：2難度：0.5
解析

1．若a=20.5，b=log32，c=log20.2，則（ ）